import pandas as pd 
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

6-1 표본과 경험적 분포 요약

url1 = "https://ilovedata.github.io/teaching/bigdata2/data/seoul_bike_201909_3.csv"
bike = pd.read_csv(url1, encoding="CP949")

개념

  • 모집단 : 분석에 필요한 전체자료
  • 표본 : 모집단의 일부분
    • 확률표본 : 단순임의추출을 통해 추출된 표본
    • 편의표본 : 개체가 표본에 포함되는 가능성을 알 수 없는 표본
  • 단순임의추출(simple random sampling) : 모집단의 모든 개체가 표본에 속할 가능성이 동일하도록 하는 추출하는 방법.
  • 경험적 분포 : 표본에 속한 데이터의 분포, 경험적이라는 의미는 추출된 관측값들의 분포라는 의미.
  • 대수의 법칙
    • 표본의 크기 증가할수록 확률표본에서 얻은 정보는 모집단에 대한 정보와 점점 가까워진다.
    • 확률표본의 경험적 분포는 표본의 수가 증가할수록 모집단의 분포와 점점 유사해진다.`
    • keyword : 확률표본,표본의 크기,증가,모집단의 분포,유사
  • 확률표본의 정확한 정의 : 모집단에 속한 개체들이 표본에 포함되는 확률이 미리 정해져 있으며 이러한 확률분포로부터 임의로 추출된 표본을 의미한다.

fake 가능성

  • 확률표본이라는 키워드가 언급되어야 함. 표본의 크기가 크면 클수록 확률표본이어야 함.
    • 그냥 표본은은 안됨. 편의표본일 수 있기 때문.

코드

  • 크키가 \(n\)인 확률표본 추출 : df.sample(n,replace = False,random_state)
    • n : 표본의 크기,replace : 복원추출여부
    • ex)bike_sample_100 = bike.sample(n=100,replace=False,random_state = 1)
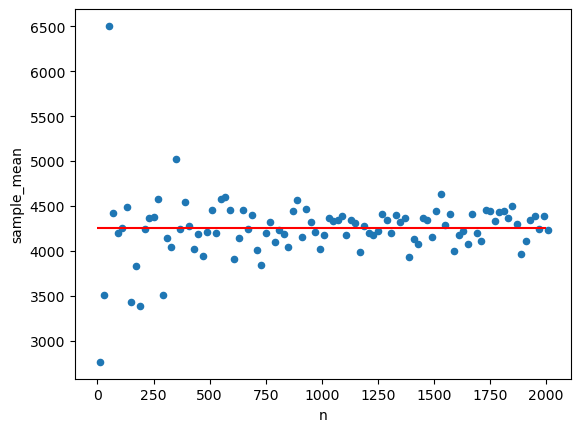
  • 표본의 크기가 점점 커지면 확룔표본의 평균이 모집단의 평균에 가까워 지는 것 시각화
    • 표본의 크기는 10에서 2010까지 20step단위로 끊어서 확인
n = np.arange(10,2021,20)
sample_mean = pd.DataFrame({"n":n,"sample_mean":np.zeros(len(n))})
#n : 다양한 표본의 크기들, 표본의 크기들이 담긴 array인 n이 value가 됨
#sample_mean : 다양한 크기의 표본에 대한 sample_mean이 담길 column, 일단 다양한 표본조합 n만큼 초기화
#n의 길이만큼 초기화, n은 지금 다양한 표본의 크기들이 들어있는 리스트
#우리는 다양한 표본의 크기에 대해서 sample mean을 계산해봐야 함.

for i,sample_size in enumerate(n):
    sample_mean.loc[i,"sample_mean"] = bike.sample(n=sample_size,replace=False)["이용거리"].mean() 
    #dataframe에서 sample하면 모든 컬럼이 전부 포함된 채로 있음
    #따라서 mean을 계산할 때, 특정컬럼을 가져와 줘야 함.
sample_mean.head(5)
n sample_mean
0 10 2763.000000
1 30 3513.333333
2 50 6504.400000
3 70 4424.285714
4 90 4201.000000 
sample_mean.plot.scatter(x="n",y="sample_mean")
plt.hlines(y=4253.336228, xmin=0, xmax=2000, colors='r')
plt.show()

6-2 통계량의 분포 요약

url1 = "https://ilovedata.github.io/teaching/bigdata2/data/seoul_bike_201909_3.csv"
bike = pd.read_csv(url1, encoding="CP949")

개념

용어 기호 정의 예
모집단(population) P 관심이 있는 전체집단 모든 선거구 주민
모집단의 수 N 전체집단에 속한 개체 수 모든 선거구 주민의 수
모수(parameter) \(\theta\) 모집단의 특성값 모집단의 지지율
표본(sample) S 모집단의 부분 집합 표본으로 추출된 주민
표본의 수 n 표본에 속한 개체의 수 표본으로 추출된 선거구 주민의 수
표본 통계량(sample statistics) \(\hat{\theta}\) 표본의 특성값 표본 지지율
  • 자료 분석의 목적 : 모집단에 대한 특성 즉 모수를 알기 위함
  • 일반적으로 자료분석은 표본에서 얻은 정보, 즉 표본통계량(=추정량)을 통해서 모수를 추론(추정)
  • 왜 자료분석을 모집단에서 안하고 표본을 추출해서 해?
    • 모집단은 크기가 너무 커서 모든 자료를 조사할 수 없음
  • 표본으로부터 계산한 통계량도 임의성을 지니며 분포를 가진다.
    • 모집단으로 부터 random하게 표본이 추출되기 때문임.
  • 통계량의 분포를 아는 것이 또 하나의 중요한 topic
    • 왜 구해야해?(시험X)
      • 통계량으로부터 모수를 추측하기 때문
  • 정확한 분포는 어떻게 구함?
    • 모집단을 정확히 알고있을때
    1. 모집단으로부터 가능한 모든 표본의 조합을 구하여
    2. 나올 수 있는 모든 표본통계량과 그에 대응하는 확률을 계산해야 함
  • 하지만 못 구하는 이유?
    • 모집단을 정확히 알아도, 가능한 조합이 경우의 수가 너무 커서 사실상 못구함
    • Q.왜 근데 조합을 먼저 취하고 구해버리냐???..?..??
  • 그렇다면 어떻게 해? \(\to\) 모의실험을 통해 경험적으로 구해볼 수 있음.
  • 경험적분포는 어떻게 구함?
    • 모집단에서 크기가 n인 표본을 뽑고
    • 표본통계량 계산하고 기록
    • 이 과정을 여러번 반복해서 표본통계량의 분포를 구해보기.
  • 표본평균의 경험적분포에 대한 매우 중요하고 신기한 특징들
    • 모집단의 분포가 정규분포를 따르지 않더라도 표본의 크기가 크면 클수록
    • 표본평균의 분포가 모양이 좌우가 대칭인 종모양(정규분포)에 가까워지며
    • 분산이 줄어든다.(퍼진정도가 줄어든다.)

fake 가능성

  • 표본의 경험적 분포 vs 표본통계량의 경험적 분포
    • 표본의 경험적 분포는 표본을 구성하는 관측값들의 분포,표본 한 개만 있어도 가능함.
    • 표본통계량의 경험적 분포는 표본에 속한 관측값들로 계산한 하나의 값,분포를 구하려면 여러개의 표본이 있어야 함.\(\to\)모의실험을 실행하는 이유
  • 반드시 확률표본이어야 한다.(비확률표본이면 절대 안된다.)

코드

(정확한 분포 구하기)

# 1. 가능한 모든 표본 구하기
from itertools import combinations

P = np.array([1,1,0,0,1])
n = 3

all_possible_samples = []
for sample in combinations(P,3):
    all_possible_samples.append(sample)

#2. 모든 표본에 대한 지지율 구하기
from fractions import Fraction

sample_rate = []
for sample in all_possible_samples:
    sample_rate.append(Fraction(sum(sample),n)) #주의,분모 분자 헷갈리면 망함
    #sample_rate.append(Fraction(len(sample)/sum(sample)))#틀린코드 

sample_rate_dist = pd.DataFrame({"sample_rate":sample_rate,"probability":np.repeat(1/len(all_possible_samples),len(sample_rate))})

sample_rate_dist.groupby("sample_rate").sum().reset_index(drop=False).rename(columns = {"sample_rate":"표본지지율"})
표본지지율 probability
0 1/3 0.3
1 2/3 0.6
2 1 0.1

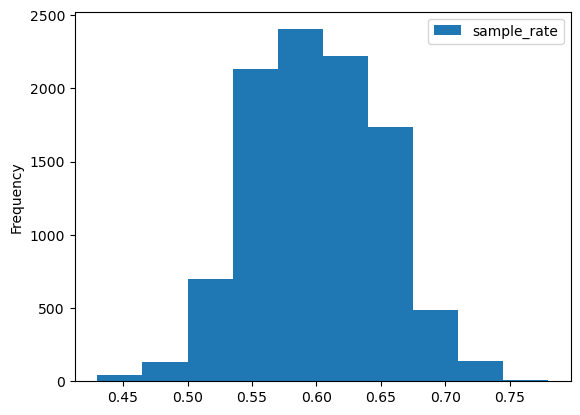
(경험적 분포구하기)

# 모집단을 만든다.
P = np.concatenate((np.ones(6000), np.zeros(4000)), axis=0)
np.mean(P)
0.6
B = 10000
n = 100

simul_sample_rates = pd.DataFrame({"sample_rate":np.zeros(B)})
for i in np.arange(B):
    sample = np.random.choice(P,n)
    simul_sample_rates.loc[i,"sample_rate"] = np.mean(sample)
simul_sample_rates.plot.hist()
<AxesSubplot:ylabel='Frequency'>

(경험적 분포 구하기 - 2) 생략

6.3 추정량의 성질

개념

  • 통계량 : 표본으로부터 계산된 요약값
  • 추정량 : 모수를 추정할 수 있는 통계량
  • 추정값 : 관측한 표본으로부터 계산한 추정량의 값
  • 추정량의 성질
    1. 추정량은 임의성을 가진다.(확률변수다.)
      • 추정량은 표본으로 계산되고, 표본이 모집단에서 임의적으로 뽑히기 때문이다.
    2. 추정량의 평균
      • 추정값들의 평균은 모수와 같다.(추정값이라고 적혀있음(추정량 X),모수는 모집단의 지지율이 였음)
      • 강의자료에서는 추정량의 평균 = 추정값들의 (표본)평균으로 설명함.
      • $ = - $, 작을수록 좋은 추정량이다.
    3. 추정량의 표준편차
      • 추정값들의 표준편차가 이렇게 된다.(공식있음)
      • 뭐 특별한건 없고 추정량도 임의성을 지니기에(random variable) 분포를 가지며 표준편차도 가진다는 점!.
  • 중심극한정리
    • 일반적으로 표본의 수가 50보다 크면 추정량의 분포가 정규분포에 꽤 가깝다.
  • 그래서 .. 중심극한정리 어디에 활용?
    • 평균으로부터 +- 2SD에 추정값이 나타날 확률이 95%
    • 위와 동일하게 추정값 +- 2SD에 평균이 나타날 확률이 95%
    • 위와 동일하게 표본지지율과 모집단 지지율의 차이가 2SD일 확률이 95%이다.
  • 표본오차는 95% 신뢰수준에서 \(\pm 3.1%\)포인트다.
    • 강의교재에서는 표본오차 = \(3.1%\)로 나왔지만 \(\theta - \hat\theta\)를 의미하는 것이라 생각함.
    • Q. 용어 상당히 헷갈림 일단 pass

코드

# 모집단의 크기
N = 100000

# 지지하는 유권자의 수 
favor = 60000

# 반대하는 유권자의 수 
opposite = 40000

# 모집단 (1=지지, 0=반대)
P = np.concatenate((np.ones(favor), np.zeros(opposite)), axis=0)
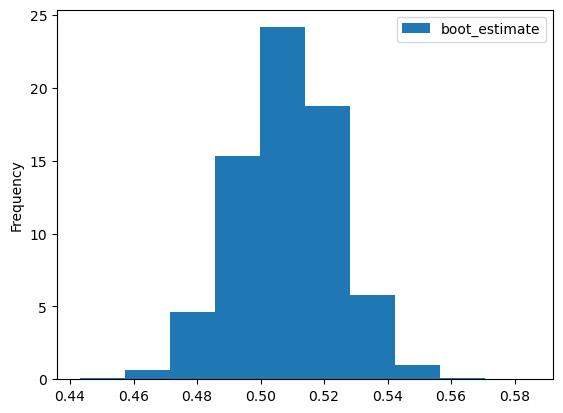
P
array([1., 1., 1., ..., 0., 0., 0.])
B = 10000
n = 1000

estimates = pd.DataFrame({"sample_rate":np.zeros(B)})
for i in np.arange(B):
    sample = np.random.choice(P,n,replace=False)
    estimates.loc[i,"sample_rate"] = np.mean(sample)
AVG = float(estimates.mean())
AVG
0.5999100999999974
SD = float(estimates.std())
SD
0.015371410020378815
[AVG - 2*SD,AVG + 2*SD]
[0.5691672799592398, 0.6306529200407551]

붓스트랩

N = 100000
theta = 0.5

favor = int(100000 * theta)
opposite = N - favor
P = np.concatenate((np.ones(favor),np.zeros(opposite)),axis=0)
n = 1000
one_sample = np.random.choice(P,n,replace=False)
one_sample[:10]
array([1., 0., 0., 0., 0., 1., 0., 1., 1., 1.])
B = 100000

bootstrap_estimates = pd.DataFrame({"boot_estimate":np.zeros(B)})
for i in np.arange(B):
    resample = np.random.choice(one_sample,n,replace=True)
    bootstrap_estimates.loc[i,"boot_estimate"] = np.mean(resample)
SD = float(bootstrap_estimates.std())
2 * SD
0.03151285719143887
lower_bound = bootstrap_estimates["boot_estimate"].quantile(0.25)
upper_bound = bootstrap_estimates["boot_estimate"].quantile(0.75)
[lower_bound,upper_bound]
[0.497, 0.519]
hat_theta = np.mean(one_sample)
lower_bound = hat_theta - 2 * SD
upper_bound = hat_theta + 2 * SD
[lower_bound,upper_bound]
[0.47648714280856114, 0.5395128571914389]
hat_theta
0.508
bootstrap_estimates["boot_estimate"].mean()
0.5080417199999819
bootstrap_estimates.plot.hist(density=True)
<AxesSubplot:ylabel='Frequency'>

url1 = "https://ilovedata.github.io/teaching/bigdata2/data/seoul_bike_201909_3.csv"
bike = pd.read_csv(url1, encoding="CP949")
bike
자전거번호 대여일시 대여 대여소번호 대여 대여소명 대여거치대 반납일시 반납대여소번호 반납대여소명 반납거치대 이용시간 이용거리
0 SPB-17003 2019-09-28 16:10:55 368 SK 서린빌딩 앞 4 2019-09-28 17:03:32 2002 노들역 1번출구 14 52 8940.0
1 SPB-14405 2019-09-28 16:48:16 2024 상도역 1번출구 3 2019-09-28 17:03:44 2002 노들역 1번출구 18 15 1910.0
2 SPB-18431 2019-09-28 16:59:54 2002 노들역 1번출구 10 2019-09-28 17:03:57 2002 노들역 1번출구 10 2 30.0
3 SPB-04853 2019-09-28 15:31:49 207 여의나루역 1번출구 앞 32 2019-09-28 17:10:12 2002 노들역 1번출구 19 98 9610.0
4 SPB-11122 2019-09-28 15:35:41 207 여의나루역 1번출구 앞 14 2019-09-28 17:10:37 2002 노들역 1번출구 18 90 9450.0
... ... ... ... ... ... ... ... ... ... ... ...
407584 SPB-24072 2019-09-12 08:56:34 240 문래역 4번출구 앞 9 2019-09-12 09:03:37 99999 영남단말기정비 2 6 720.0
407585 SPB-16130 2019-09-18 10:13:09 99999 영남단말기정비 1 2019-09-18 11:38:30 99999 영남단말기정비 1 85 40.0
407586 SPB-03728 2019-09-25 08:00:28 2183 동방1교 7 2019-09-25 08:54:02 99999 영남단말기정비 5 53 12910.0
407587 SPB-08928 2019-09-30 07:49:27 2183 동방1교 10 2019-09-30 09:42:27 99999 영남단말기정비 7 2 0.0
407588 SPB-06988 2019-09-30 09:58:43 99999 영남단말기정비 5 2019-09-30 13:01:26 99999 영남단말기정비 5 182 10.0

407589 rows × 11 columns

bike2 = bike[ ["이용시간","이용거리"] ].rename(columns={"이용시간":"time", "이용거리":"distance"})
bike2
time distance
0 52 8940.0
1 15 1910.0
2 2 30.0
3 98 9610.0
4 90 9450.0
... ... ...
407584 6 720.0
407585 85 40.0
407586 53 12910.0
407587 2 0.0
407588 182 10.0

407589 rows × 2 columns

bike2.describe()
time distance
count 407589.000000 407589.000000
mean 30.156827 4253.336228
std 32.065934 5782.673901
min 1.000000 0.000000
25% 8.000000 1200.000000
50% 18.000000 2380.000000
75% 43.000000 5130.000000
max 2479.000000 153490.000000 
n=1000
one_sample = bike2.sample(n=1000,replace=False)
one_sample.describe()
time distance
count 1000.000000 1000.000000
mean 29.573000 4295.160000
std 31.391944 6355.280258
min 1.000000 0.000000
25% 8.000000 1230.000000
50% 17.000000 2355.000000
75% 43.000000 5035.000000
max 245.000000 86470.000000 
B = 1000

estimates = pd.DataFrame({"time_estimates":np.zeros(B),"distance_estimates":np.zeros(B)})
for i in np.arange(B):
    estimates.loc[i,"time_estimates"] = one_sample["time"].sample(n,replace=True,random_state = i).median()
    estimates.loc[i,"distance_estimates"] = one_sample["distance"].sample(n,replace=True,random_state = i).median()
estimates
time_estimates distance_estimates
0 18.0 2430.0
1 17.0 2300.0
2 18.0 2340.0
3 17.0 2305.0
4 17.0 2290.0
... ... ...
995 18.0 2360.0
996 16.0 2220.0
997 17.0 2400.0
998 16.0 2345.0
999 17.0 2290.0

1000 rows × 2 columns

estimates["time_estimates"].quantile(0.025),estimates["time_estimates"].quantile(0.975)
(16.0, 20.0)
float(estimates["distance_estimates"].quantile(0.025)),estimates["distance_estimates"].quantile(0.975)
(2190.0, 2565.125)