Text(0.5, 1.0, 'n=200')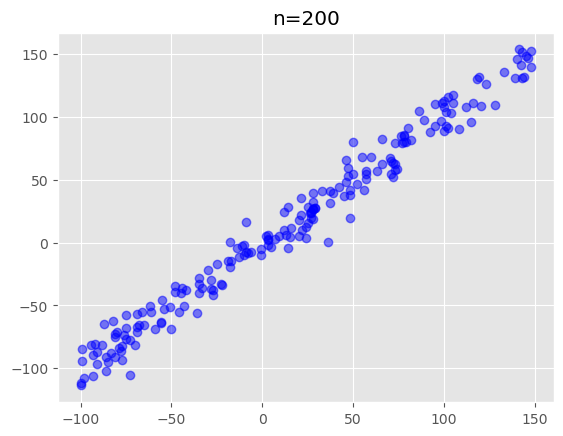
신호연
December 24, 2022
선형회귀에 대해서 정리한 글입니다.
선형회귀는 변수사이의 관계가 선형이라고 가정했을 때, 독립변수로 연속형 변수인 종속변수의 값을 예측하기 위한 문제에서 사용합니다.
데이터셋이 m개의 독립변수를 가지며 1개의 연속적인 종속변수를 가진다고 가정합시다. 우리의 목적은 x를 입력으로 하고 y값을 예측하는 모형을 만드는 것이 목적입니다.
\[\begin{aligned} &\text{Given, }D = \{(x_{i,1},x_{2,i},\dots,x_{M,i},y_i)\}_{i=1}^{i=N} \\ &\text{Goal : unseendata에 대해서 x를 입력으로 연속형변수 y값을 예측하는 선형모형만들기} \end{aligned}\]선형회귀는 독립변수와 종속변수사이의 관계를 선형(일차식,직선,평면)으로 모델링하여 독립변수\(x\)를 입력으로 연속형변수인 종속변수 \(y\)값을 예측하는 문제에 활용됩니다. 선형회귀는 가장 간단한 예측모형으로 선형회귀의 핵심아이디어를 모방하여 다른 모형에서도 활용합니다.
Text(0.5, 1.0, 'n=200')
우리가 가진 데이터를 관찰해봅시다. 가장크게 눈에 띄는 사실은 x와 y사이의 관계가 선형적이라는 점입니다. 따라서 간단한 선형모형으로 독립변수와 종속변수사이의 관계를 모델링할 수 있을 것 같습니다. 조금 더 세부적으로 들어가서 각각의 x값에 대해서 y값을 관찰해 봅시다. 첫번째로 알 수 있는 점은 동일한 x값에 대해서도 서로다른 y값을 가지는 점들 데이터가 많이 있다는 것입니다. 이로부터 \(y\)가 \(x\)뿐만아니라 또다른 확률변수 \(\epsilon\)의 값에 의해 결정된다는 것을 알 수 있습니다. 두번째로 x값에 의해서 찍히는 점의 위치(y)의 양상이 다르다는 점을 알 수 있습니다. x가 작으면 일반적으로 y는 낮은위치에서 점이 찍히고 x가 크면클수록 일반적으로 높은 위치에서 점이 찍히는 것을 알 수 있습니다.
데이터를 관찰하면서 얻은 사실로부터 \(x\)와 \(y\)사이의 관계를 수학적으로 모델링 해보겠습니다. 첫번째 사실로부터 우리는 동일한 \(x\)라도 각각의 데이터에 대해서 어떤 또다른 값이 더해짐을 알 수 있습니다. 이렇게 뽑힐때마다 그 값이 다른 변수는 확률변수 \(\epsilon_i\)를 더해줌으로서 표현할 수 있습니다. 여기서 오차가 따르는 분포에 대해서 가정을 합니다. 오차는 평균이 0이고 분산이 \(\sigma^2\)인 정규분포를 따르는 확률변수라고 가정합니다.
또한 두번째 사실로부터 우리는 \(x\)와 \(y\)는 커지면 커지고 작아지면 작아지는 관계임을 알 수 있습니다. 이러한 관계를 표현할 수 있는 방법은 여러가지가 있지만 선형회귀에서는 선형으로 이 관계를 표현합니다.
\[\begin{aligned} &Y_i = w_0 + w_1x_1 + \dots + w_Mx_M + \epsilon_i={\bf{x_i}^\intercal}w + \epsilon_i\\ &\text{where , }{\bf{{\bf{x_i}^\intercal}}} = \begin {bmatrix}0,x_{i,1},\dots,x_{i,M} \end {bmatrix} \in \mathbb{R^{1 \times (M+1)},{\bf{w}} = \begin {bmatrix} w_0,w_1,\dots,w_M\end{bmatrix}}^\intercal \in \mathbb{R^{(M+1)\times 1}}\\ \quad\quad\quad &\epsilon_i \overset{i.i.d}{\sim} \mathcal{N}(0,\sigma^2)\,\,(\text{for } i=1,2,\dots,N) \end{aligned}\]이렇게 \({\bf{x_i}^\intercal}\)와 \(Y_i\)사이의 관계를 정할 경우 각각의 \(Y_i\)안에 확률변수 \(\epsilon_i\)가 \(Y_i\)도 마찬가지로 정규분로를 따르는 확률변수로 그 값이 \(\epsilon\)에 의해 독립변수의 값이 동일하더라도 추출할때마다 다를 수 있습니다. \(Y_i\)도 확률변수이므로 정규분포를 따르는 확률변수이므로 중심위치와 변동을 확인하기 위해 기댓값과 분산을 구해볼 수 있습니다. 이때 \(x\)는 주어져 있으므로 그때의 확률분포에 대해서 계산하면 다음과 같습니다.
\[\begin{aligned} &\mathbb{E}[Y_i] = \mathbb{E}[w_0 + \dots + w_Mx_M+\epsilon_i] = w_0 + w_1x_1 + \dots + w_Mx_M={\bf{x_i}^\intercal}w \\ &\text{var}[Y_i] = \text{var}[w_0 + \dots + w_Mx_M+\epsilon_i] = \text{var}[\epsilon_i] = \sigma^2 \end{aligned}\]위수식으로부터 각각의 \(Y_i\)에 대한 확률분포는 정규분포이며(\(\epsilon_i\)에 의해) 기댓값은 \(x\)와 \(w\)에 의해 정해지지만 분산은 \(\sigma^2\)으로 항상 동일하다는 점을 알 수 있습니다. 모두 정규분포를 따르지만 기댓값만 \(x\)에 의하여 달라집니다. 즉 다음과 같습니다.
\[\begin{aligned} &Y_i|w;{\bf{x_i}^\intercal} \sim \mathcal{N}({\bf{x_i}^\intercal}{\bf{w}},\sigma^2)\, \text{ for } i = 1,2,\dots,N\\ &p(y_i|{\bf{w}};{\bf{x_i}^\intercal}) = 정규분포식 \end{aligned}\]여기까지 우리가 가진 데이터를 기반으로 독립변수와 종속변사이의 관계를 선형모형을 만들어봤습니다. 그렇다면 궁극적인 목적인 unseen data에 적절하게 종속변수의 값을 예측하려면 어떻게 해야할까요?만약 학습데이터로부터 적절히 가중치인 \(w\)를 구할수만 있다면 독립변수가 입력되었때 대하여 종속변수가 따르는 확률분포(정규분포)를 알 수 있고 그 분포에서 가장 확률이 높은 곳의 종속변수의 값(정규분포에서는 xw)을 예측값으로 하면 됩니다. 또 다르게 생각하면 가중치를 구한다는 것은 데이터를 가장 잘 표현하는 직선(평면,초평면)을 얻은것이므로 입력x에 대하여 직선의 값을 읽어서 예측값으로 하면 됩니다. 어찌됐건 두 경우 모두 가중치를 구해야**하므로 우리의 목적은 이제 가중치를 구하는 것입니다.
그렇다면 가장 적절한 가중치는 무엇일까요? 데이터가 주어질때 가중치에 확률이 다음과 같다고 해봅시다.
\[\begin{aligned} &p({\bf{w}}|D) = p_{{\bf{w}}|Y_1,Y_2,\dots,Y_N}(w|y_1,y_2,\dots,y_N;{\bf{X}})\\ &\text{where, } {\bf{X}} = \begin{bmatrix} --{\bf{x_1^\intercal}}--\\ --{\bf{x_2^\intercal}}--\\ \vdots\\ --{\bf{x_N^\intercal}}-- \end{bmatrix} \end{aligned}\]오른쪽식은 왼쪽식에서의 데이터\(D\)를 좀더 풀어적은 수식입니다. 만약 위와 같은 확률을 계산했을때 그 값이 작은 가중치는 가능성이 낮은 가중치이므로 우리가 찾는 적절한 가중치는 아닐것입니다. 반대로 확률이 높은 가중치는 가능성이 높은 가중치이기때문에 우리가 찾는 가중치라고 할 수 있겠습니다. 그러면 그냥 “저 확률을 가장 크게 하는 가중치를 찾으면 되겠다”라고 생각이 들지만 안타까운 점은 우리는 위와같은 (조건부)확률(분포)을 바로 알기가 어렵습니다.. 따라서 베이즈정리의 도움을 받습니다. 베이즈 정리는 다음과 같습니다.
\[\begin{aligned} &p({\bf{w}}|D) = \frac{p(D|{\bf{w}})p({\bf{w}})}{p(D)} \propto (D|{\bf{w}})p({\bf{w}}) \end{aligned}\]수식에서 분모\(p(D)\)는 normalization constant라 하는 상수입니다. 그러므로 분자를 최대화하는 가중치를 구하면 되지만 MLE(maximum likelyhood estimation) 에서는 likelyhood인 \(L = p(D|w)\)만을 최대화 하는 것을 목적으로 합니다.
log likelyhood를 구하면 다음과 같습니다. 로그를 취하는 이유는 최댓값을 가지는 \({\bf{w}}\)가 변하지 않고 곱셈을 덧셈을 바꿔서 계산하기 더 편하기 때문입니다.
\[\begin{aligned} \text{lnL} &= \text{ln}\prod_{n=1}^N \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{(y_n-{\bf{x_n}}^\intercal{\bf{w}})^2}{2\sigma^2} \right\} \\ &= \sum_{n=1}^N\text{ln} \frac{1}{\sqrt{2\pi \sigma^2}}\text{exp}\left\{-\frac{(y_n-{\bf{x_n}}^\intercal{\bf{w}})^2}{2\sigma^2} \right\} \\ &= \sum_{n=1}^N \text{ln}\frac{1}{\sqrt{2\pi\sigma^2}} - \frac{1}{2\sigma^2} \sum_{n=1}^{N}(y_n-{\bf{x_n}}^\intercal{\bf{w}})^2 \\ &= C_1 - C_2\sum_{n=1}^{N}(y_n-{\bf{x_n}}^\intercal{\bf{w}})^2 \end{aligned}\]상수를 제외해도 최댓값의 위치는 변하지 않으므로 제외하고 loglikelyhood를 최대화 하는 가중치를 얻은것이 우리의 목표입니다. 이때의 가중치는 가중치에 대한 추정량이므로 \(\bf{\hat{w}}\)로 표기합니다.
여기서 시그마에서부터 보면 흔히 경사하강법에서 쓰는 MSE가 보입니다. MSE는 선형회귀의 MLE에서 Negative log likelyhood를 구할때 나오는 항입니다.
psuedo inverse에 의한 해를 구하면 다음과 같습니다.
\[\begin{aligned} \hat{{\bf{w}}} = (\bf{X^TX}^{-1})X^Ty \end{aligned}\]경사하강법은 \(\bf{w}\)를 구하는 방법입니다. 경사하강법의 대략적인 흐름을 요약하면 다음과 같습니다.

그림출처 : https://www.kdnuggets.com/2020/05/5-concepts-gradient-descent-cost-function.html
(경사하강법의 대략적인 흐름)
1. \(\bf{W}\)의 추정값 \(\hat{\bf{W}}\)을 임의적으로 가정(초기화)한다.
2. 가정한 \(\hat{\bf{W}}\)로 \(\hat{\bf{y}}\)(\(\bf{y}\)에 대한 추정값)을 구하여 실제값\(\bf{y}\)와 얼마나 비슷하지 않은지,틀린지 확인한다. => Loss function의 역할입니다.
3. 기울기(편미분계수,gradient)를 사용하여 \(\hat{\bf{W}}\)을 수정한다.많이 틀리면 많이수정하고 적게틀리면 적게 수정한다.
4. 2번,3번을 계속해서 반복한 후 어느정도 적게 틀리면 종료한다..
2번에서 구한 추정값 \(\hat{\bf{W}}\)이 얼마나 틀린지,부정확한지 알려주는 함수를 Loss function 또는 Cost function이라고 합니다. 선형회귀에서의 Loss function은 일반적으로 MSE를 사용하며 주어진 샘플에서 잔차(residual,\(\hat{y}_i-y\))들을 전부 제곱하여 더한 값입니다.
(Loss function)
\(MSE = \Sigma_{i=1}^{i=n}(y_i - \hat{y_i})^{2} = \frac{1}{n}({\bf{y} - \bf{\hat{y}}})^{T}({\bf{y} - \bf{\hat{y}}}) = \frac{1}{n}(\bf{y}-X\hat{\bf{W}})^{T}(\bf{y}-X\hat{\bf{W}})\)
MSE와 같은 Loss function은 우리의 추정이 얼마나 틀렸는지를 나타내는 \(\hat{\bf{W}}\)에 대한 함수입니다. 그러므로, loss function을 가장 최소화 하는 \(\bf{\hat{W}}\)을 찾아내면 확률변수사이의 선형관계인 \(\bf{W}\)를 알아낼 수 있습니다.
Text(110, 15, 'residual')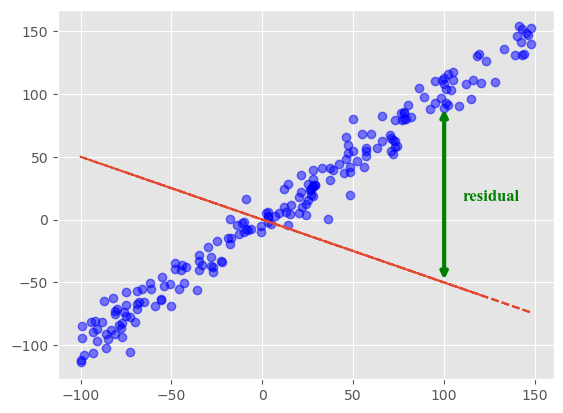
n개의 독립변수를 가지는 다변수 스칼라 함수에 대한 Gradient는 수학적으로 다음과 같습니다.
\(\nabla_{X}{f(x_1,x_2,...,x_n)} = (\frac{\partial f}{\partial x_1},\frac{\partial f}{\partial x_2},\dots,\frac{\partial f}{\partial x_n})\)
다변수 스칼라 함수에 그레디언트를 취하면 벡터입니다.그러므로,그레디언트를 벡터(다변수)를 입력했을 때,벡터를 출력으로 하는 벡터함수라고 생각해도 무방합니다.중요한 사실은 임의의 공간상의 임의의 point \(X\)에서 스칼라함수에 대한 gradient of f = \(-\nabla_{X}{f}\) 방향은 스칼라함수가 가장 급격하게 감소하는 방향이라는 사실입니다.(증명생략)
위의 사실에 의하면,우리는 임의의 \(\hat{\bf{W}}\)에서 Loss function이 가장 급격하게 감소하는 방향을 찾을 수 있습니다. 그러므로 감소하는 방향을 찾고 이동하고 감소하는 방향을 찾고 이동하고 반복하다보면… 궁극적인 목적인 틀린정도를 최소화하는 즉,Loss function값이 가장 작은 \(\hat{\bf{W}}\)를 찾을 수 있습니다. \(\bf\hat{W}\)를 수정하는 구체적인 수식은 다음과 같습니다.
(Gradient descent parameter update)
\(\hat{\bf{W}}_{t} = \hat{\bf{W}}_{t-1} - \alpha\times\nabla_{W}{L}\)
\(\hat{\bf{W}}_{t-1}\)은 수정되기전의 가중치(벡터)이며 \(\hat{\bf{W}_{t}}\)는 파라미터를 한번 업데이트 한 후의 가중치(벡터)입니다. \(t-1\)의 \(\hat{\bf{W_{t-1}}}\)에 \(-\alpha\times\nabla_{W}{L}\)를 더해줌으로서 \(\hat{\bf{W}}_{t-1}\)은 loss function이 가장 급격히(많이)감소하는 방향으로 이동하며 \(\hat{\bf{W}}_{t}\)가 됩니다. \(\alpha\)는 학습률(learning rate)입니다. \(\hat{\bf{W}}_{t-1}\)과 곱해져서 얼마나 많이 또는 적게 움직일지를 결정합니다. 한번에 얼마나 이동할지에 비유한 “보폭”으로 생각할 수 있습니다.
요약하자면, 경사하강법을 통하여 위와 같이 가중치\(\hat{\bf{W}}\)를 재귀적으로 업데이트 하면 loss function \(L\)이 가장 최소가 되는 지점의 \(\hat{\bf{W}}\)를 찾을 수 있습니다.
MSE를 더 상세히 전개하면 다음과 같습니다.
\(MSE = \Sigma_{i=1}^{i=n}(y_i - \hat{y_i})^{2}\)
\(= \frac{1}{n}({\bf{y} - \bf{\hat{y}}})^{T}({\bf{y} - \bf{\hat{y}}})\)
\(= \frac{1}{n}(\bf{y}-X\hat{\bf{W}})^{T}(\bf{y}-X\hat{\bf{W}})\)
\(= \frac{1}{n}(\bf{y^T - \hat{\bf{W}}^{T}\bf{X}^{T})(\bf{y} - \bf{X}\bf{\hat{W}}})\)
\(= \frac{1}{n}(\bf{y^Ty-y^TX\hat{W}} - \hat{W}X^Ty + \hat{W}^TX^TX\hat{W})\)
여기서 \(\bf{y^TX\hat{W}} \in \bf{R}^{1 \times 1}\) 이므로 \(\bf{y^TX\hat{W}} = (\bf{y^TX\hat{W}})^T = (\bf{\hat{W}X^Ty})\)가 성립합니다. 그러므로 MSE를 정리하면 다음과 같습니다.
(MSE)
\(MSE = \frac{1}{n}(\bf{y^Ty -2\hat{W}X^Ty + \hat{W}^TX^TX\hat{W}})\)
(Gradient of MSE)
\(\nabla{L} = MSE\)
\(= \bf{\frac{1}{n}\frac{\partial}{\partial \hat{W}}(\bf{y^Ty - 2\hat{W}^TX^T + \hat{W}^TX^TX\hat{W}})}\)
\(= \bf{\frac{1}{n}}(\bf{\frac{\partial}{\partial \hat{W}}}{y^{T}y} - \frac{\partial}{\partial \hat{W}}2\hat{W}^{T}X^{T}y + \frac{\partial}{\partial\hat{W}}\hat{W}^{T}X^{T}X\hat{W})\)
\(= \bf{\frac{1}{n}(\frac{\partial}{\partial \hat{W}}{y^{T}y} - \frac{\partial}{\partial \hat{W}}2y^TX\hat{W} + \frac{\partial}{\partial\hat{W}}\hat{W}^TX^TX\hat{W})}\)
\(= \bf{\frac{1}{n}[0 - 2X^Ty + (X^TX + X^TX)\hat{W}]}\)
\(= \bf{\frac{2}{n}X^T(X\hat{W} - y)}\)
(parameter update)
\(\bf{\hat{W}_{t} = \hat{W}_{t-1} - \alpha \times \frac{2}{n}X^T(X\hat{W} - y)}\)
모집단의 두 확률변수사이의 관계가 다음과 같다고 가정해봅시다.
\(y = 2.5 + 3x + \epsilon\)
모집단에서 크기가 n인 표본을 뽑으면 다음과 같습니다.
#n=200인 표본 추출
n=200
torch.manual_seed(2202)
W = torch.tensor([0,1]).reshape(2,-1).float()
_x = torch.randint(-100,150,(n,1))
_ones = torch.ones((n,1))
_epsilon = torch.randn((n,1)) * 10 #변동을 조금 더 주기 위해서 오차를 곱해줌
X = torch.concat((_ones,_x),axis=1).float()
y = X @ W + _epsilon
plt.plot(X[:,1],y,"bo",alpha=0.5)
plt.title("n=200")Text(0.5, 1.0, 'n=200')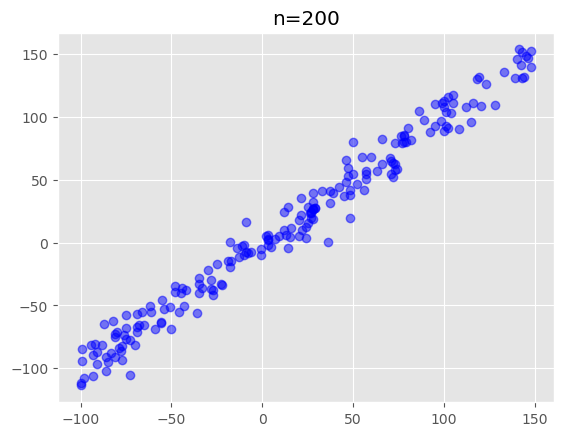
경사하강법으로 표본에 가장 잘 맞는 직선을 찾아봅시다.
먼저 임의의 \(\bf{\hat{w}} = (w_0,w_1)=(0,-5)\)로 가정합니다.
#1. 먼저 임의의 W_hat을 가정한다.
W_hat = torch.tensor([0,-5]).reshape(2,-1).float()
#시각화코드
plt.plot(X[:,1],y,"bo",alpha=0.5)
plt.plot(X[:,1],X@W_hat,"g--")
plt.title("initializing What")Text(0.5, 1.0, 'initializing What')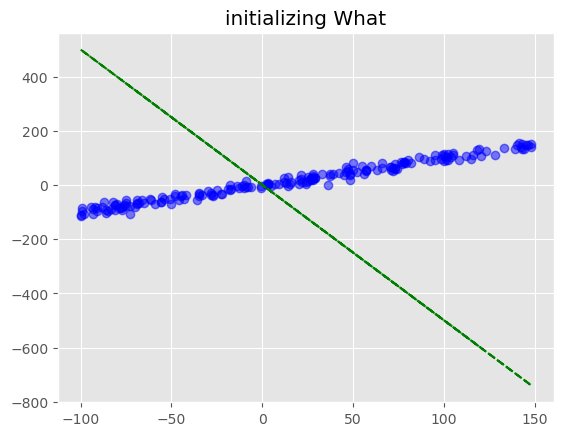
#n=100인 표본 추출
n=200
torch.manual_seed(2202)
W = torch.tensor([0,1]).reshape(2,-1).float()
_x = torch.randint(-40,25,(n,1))
_ones = torch.ones((n,1))
_epsilon = torch.randn((n,1))*5 #변동을 조금 더 주기 위해서 오차를 곱해줌
X = torch.concat((_ones,_x),axis=1).float()
y = X @ W + _epsilon
#plt.plot(X[:,1],y,"go",alpha=0.5)
#1. 먼저 임의의 W_hat을 가정한다.
W_hat = torch.tensor([0,-5]).reshape(2,-1).float()
#2.loss 를 계산한다.
#2.1
#pytorch의 MSELoss 클래스로 loss_fn이라는 객체(object)를 만듭니다.
#이 객체는 호출(call)하여 MSE를 계산할 수 있습니다
loss_fn = torch.nn.MSELoss()
yhat = X @ W
#2.2
#call하여 MSE를 계산
loss = loss_fn(yhat,y)
print(loss)
#3.파라미터를 업데이트 한다
print("업데이트 전 W_hat :",W_hat)
plt.plot(X[:,1],y,"bo",alpha=0.5)
plt.plot(X[:,1],X@W_hat,"g--")
W_hat.data = W_hat.data - 1e-1 * loss.data
print("파라미터 한 번 업데이트 후 W_hat :",W_hat)
plt.plot(X[:,1],X@W_hat,"r--")
plt.legend(["samples","before update","after one update"])tensor(27.4176)
업데이트 전 W_hat : tensor([[ 0.],
[-5.]])
파라미터 한 번 업데이트 후 W_hat : tensor([[-2.7418],
[-7.7418]])<matplotlib.legend.Legend at 0x26c127302e0>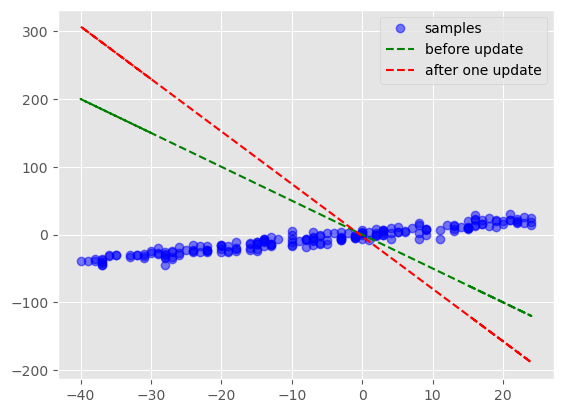
경사하강법의 흐름을 따라서 파이토치에서 구현하기위해 4가지 과정이 필요합니다.
1)\(\bf{\hat{y}}\)
2)loss
3)derivative
4)update & clean
위와 같이 파라미터를 업데이트 한 방식을 여러번 반복하면 알맞은 직선을 얻을 수 있습니다.여기서는 위의 절차를 다 수행하지 않고 최종적으로 정리해놓은 MSE에 대한 미분을 활용하여 구현해보겠습니다.
torch.manual_seed(2202)
W = torch.tensor([0,1]).reshape(2,-1).float()
_x = torch.randint(-40,25,(n,1))
_ones = torch.ones((n,1))
_epsilon = torch.randn((n,1))*5 #변동을 조금 더 주기 위해서 오차를 곱해줌
X = torch.concat((_ones,_x),axis=1).float()
y = X @ W + _epsilon
#plt.plot(X[:,1],y,"go",alpha=0.5)
#1. 먼저 임의의 W_hat을 가정한다.
W_hat = torch.tensor([0,-5]).reshape(2,-1).float()
#상세히 전개한 parameter update수식 사용.
#2~4반복
plt.subplots(1,5,figsize=(50,20))
i=1
for epoch in range(1000):
#1~3 yhat,loss,derivative(gradient) skip
#4 update
W_hat.data = W_hat.data - (1e-5 * 2/n * X.T@(X@W_hat - y)).data #직선의 변화를 관찰하기위한 작은 학습률
#시각화코드
if epoch % 100 == 0:
plt.subplot(2,5,i)
plt.plot(X[:,1],y,"bo",alpha=0.5)
plt.plot(X[:,1],X@W_hat,"r--")
t = W_hat.data
text=f"What = ({round(t[0].tolist()[0],3)},{round(t[1].tolist()[0],3)})"
plt.title(text)
i+=1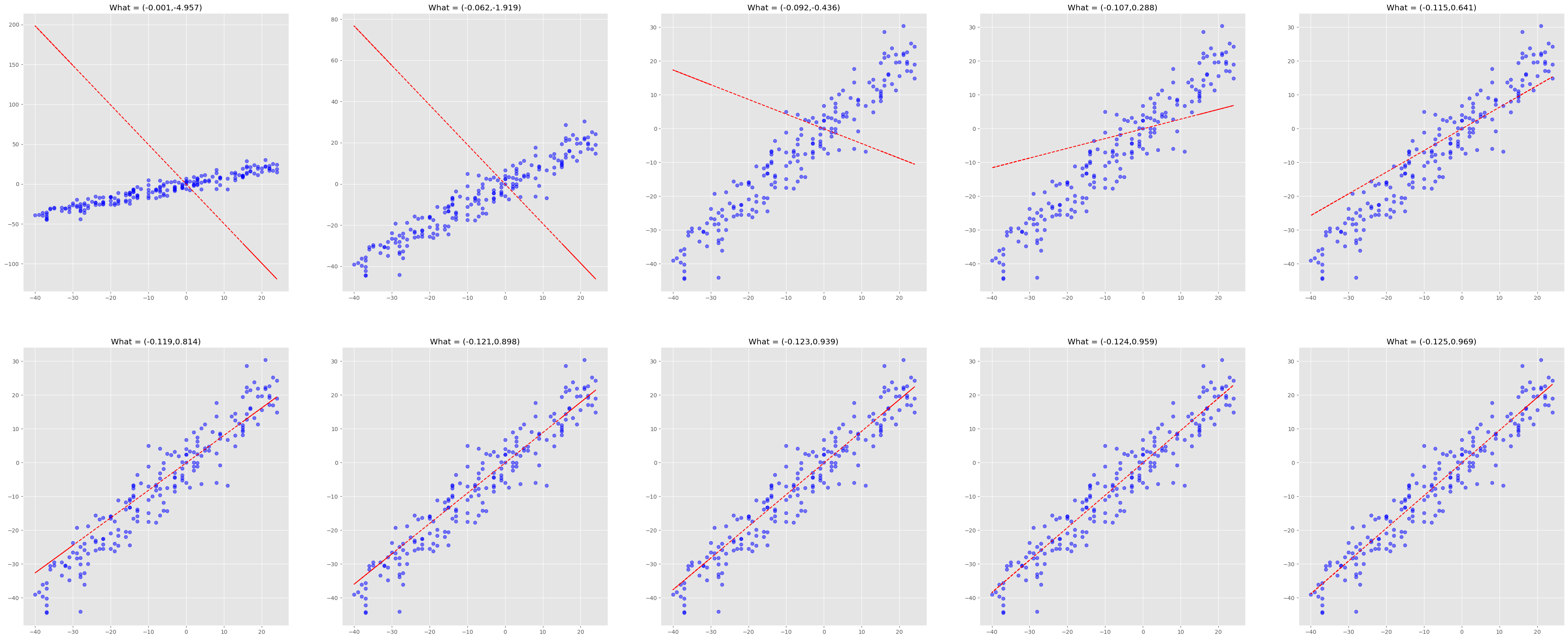
200개의 샘플로부터 \(\bf{w}\)를 추정하여 \(\hat{\bf{w}}= (0.125,0.969)\)를 얻었습니다. population regression model의 \({\bf{w}} = (w_0,w_1) = (0,1)\)을 올바르게 추정했음을 알 수 있습니다. 아주 약간의 차이가 존재하는데 이 차이는 모집단에서 샘플을 더 얻거나 더 세밀하게 업데이트하면 최소화할 수 있습니다.
#plt.title("w_1 : {} // w_0: {}".format(round(W_hat[1].tolist()[0],3),round(W_hat[0].tolist()[0],3)))
plt.title("Linear Regression")
text=f"What = ({round(t[0].tolist()[0],3)},{round(t[1].tolist()[0],3)})"
plt.plot(X[:,1],y,"bo",alpha=0.5)
plt.plot(X[:,1],X@W_hat,"r--")
plt.gca().axes.xaxis.set_visible(False)
plt.gca().axes.yaxis.set_visible(False)
plt.title(text)Text(0.5, 1.0, 'What = (-0.125,0.969)')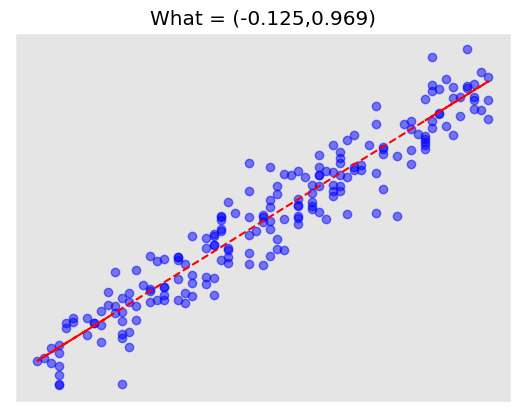
Maximum Likelihood Estimation(MLE) & Maximum A Posterior(MAP)