유투브 - 혁펜하임님의 선형대수학강의를 정리하기 위해 작성한 글입니다.Rank와 Null space로 Ax=b의 해의 갯수를 파악합니다.
연립일차방정식은 행렬 Ax=b로 나타내고 행렬의 랭크와 열공간을 기반으로 해의 갯수를 나타낼 수 있습니다.
열공간을 기반으로 한 Ax=b의 해석
행렬\(A = \begin{bmatrix}a_1 & a_2 & \dots & a_n\end{bmatrix} \in \mathbb{R}^{m \times n}\)와 벡터\(x = \begin{bmatrix}x_1,x_2,\dots,x_n\end{bmatrix}^T\in \mathbb{R}^{n \times 1}\)의 곱을 생각해보자. 행렬과 벡터의 곱은 다음과 같이 열벡터의 일차결합으로 바라볼 수 있다.
행렬 A의 열공간은 열벡터들의 선형생성이다.
\[\begin{aligned} &\text{C}(A) = \text{span}(a_1,a_2,\dots,a_n) = \{c_1a_1 + c_2a_2 + \dots c_na_n|c_1,c_2,\dots,c_n \in K\} \end{aligned}\]그러므로, 행렬 \(A\)의 열공간은 임의의 \(x\)에 대하여 가능한 \(Ax\)의 모든 집합과 같다. 가능한 모든 스칼라\(x_1,x_2,\dots,x_n\)로 벡터의 일차결합이 이루는 집합은 생성(span)과 같기 때문이다.
\[\text{C}(A) = \text{span}(a_1,a_2,\dots,a_n) = \{Ax |x\in K^n\}\]
만약 \(Ax = b\)인 방정식의 해 \(x\)를 구하려 한다 하자. \(\text{C}(A)\)는 가능한 \(Ax\)의 모든 집합이였으므로 만약 \(\text{C}(A)\)가 \(b\)를 포함한다면(즉,\(b\)가 열공간의 원소라면) \(Ax=b\)인 \(x\)가 존재하여 방정식의 해가 존재하고 \(\text{C}(A)\)가 \(b\)를 포함하지 않는다면 \(Ax = b\)인 \(x\)값이 존재하지 않고 따라서 방정식의 해가 존재하지 않는다.
Case1 : A가 full column rank일 때
문제 : \(A \in \mathbb{R}^{m \times n},\text{rank}(A) = n<m\,,x = \in \mathbb{R}^{n \times 1}\,,b\in \mathbb{R}^{m \times 1}\) 일때, \(Ax = b\)를 만족하는 x의 갯수는?
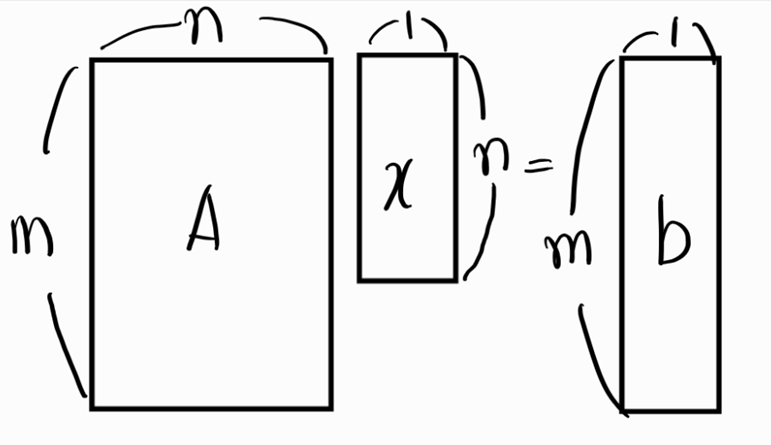 위의 문제에서 A는 full column rank이다. full column rank일 경우 \(Ax\)의 모양은 위와 같고 열공간은 m차원 벡터공간의 부분공간이자 n차원 벡터공간이다.앞에서 “m차원 벡터공간의 부분공간인 n차원 벡터공간” 이라 했는데 그 이유는 (열)벡터가 m차원 벡터공간의 원소(벡터)이기 때문이다. m차원 벡터공간에 있는 (열)벡터 n개를 기저로 생성된 공간이기 때문에 m차원 벡터공간의 부분공간이면서 동시에 n차원 벡터공간이 된다.
위의 문제에서 A는 full column rank이다. full column rank일 경우 \(Ax\)의 모양은 위와 같고 열공간은 m차원 벡터공간의 부분공간이자 n차원 벡터공간이다.앞에서 “m차원 벡터공간의 부분공간인 n차원 벡터공간” 이라 했는데 그 이유는 (열)벡터가 m차원 벡터공간의 원소(벡터)이기 때문이다. m차원 벡터공간에 있는 (열)벡터 n개를 기저로 생성된 공간이기 때문에 m차원 벡터공간의 부분공간이면서 동시에 n차원 벡터공간이 된다.
위에서 언급했듯이 열공간은 임의의 x에 대하여 가능한 \(Ax\)의 집합이기에 방정식의 해가 존재하려면 b가 열공간안에 있으면 되고 아니면 바깥에 있으면 된다. 그렇다면 이 경우 b의 위치는 어떻게 될까?
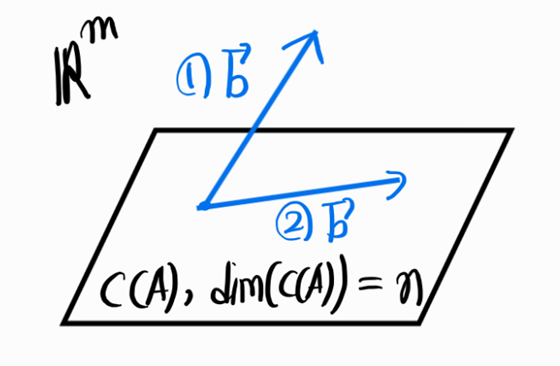
가능한 b의 위치는 2가지이다. 1의 경우는 열공간안에 b가 없는 경우다. 이 경우 b는 m차원 벡터공간에는 있으면서(\(b \in R^{m \times 1}\)이기에 당연하다) 부분공간인 n차원 열공간안에는 없게된다. 따라서 이 경우 해는 존재하지 않는다. 2의 경우는 열공간안에 b가 있는 경우다. 이 경우 b는 m차원 벡터공간에 속하면서 동시에 부분공간인 n차원 벡터공간에도 속한다.
이렇게 생각하면 끝난 것 같은데 한가지 더 생각해야 할 것이 있다. 바로 null space이다. 만약 Ax = b를 만족하는 하나의 해인 \(x_{particular}\)가 있다고 해보자. 이때 \(Ax=0\)을 만족하는 널공간의 임의의 원소인 \(x\)를 \(x_{null}\in N(A)\)이라고 하면 다음이 성립한다.
\[A(x_{particular} + x_{null}) = Ax_{particular} + Ax_{null} = b\]
윗식에 의해서 null space의 원소인 \(x_{null}\)과 \(x_{particular}\)의 합도 방정식의 해이므로 해를 구할때 null space도 확인해야 한다. null space에 대한 x를 추가한 완전해는 다음과 같다.
\[x_{complete} = x_{particular} + x_{null}\]
그렇다면 x_{null}을 어떻게 확인할 수 있을까? 랭크-널리티 정리로 확인할 수 있는데 위와같이 full column rank인 경우는 다음과 같다.
랭크-널리티 정리에 의하여 null space의 차원이 0임을 확인했다. 차원이 0인 널공간(벡터공간)은 \(\{\bf{0}\}\)이므로 \(x_{null} \in N(A)\)인 \(x_{null} ={\bf 0}\)이다.
따라서 2번의 경우, \(x_{particular}\)가 존재하여 \(Ax = 0\)일 경우의 완전해는 다음과 같다.
\[\therefore x_{total} = x_{particular} + x_{null} = x_{particular} + {\bf 0} = x_{particular}\]
결론적으로, full column rank일 경우 해가 존재하지 않거나 단 하나 존재한다.
Case2 : A가 full row rank일 때
문제 : \(A \in \mathbb{R}^{m \times n},\text{rank}(A) = m<n\,,x = \in \mathbb{R}^{n \times 1}\,,b\in \mathbb{R}^{m \times 1}\) 일때, \(Ax = b\)를 만족하는 x의 갯수는?
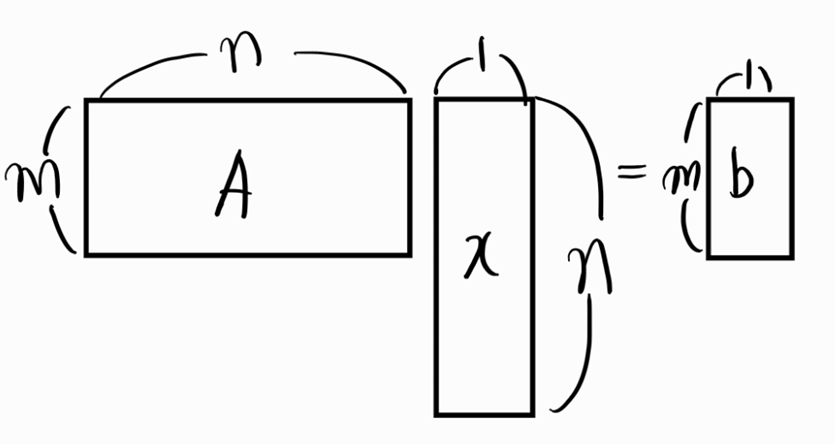 위의 문제에서 A는 full row rank이다. 위해서 한 것처럼 먼저 \(C(A)\)와 \(b\)가 어떻게 위치하고 있을지 파악하고 null space를 따져 완전해를 구하는 것이다. 먼저 \(C(A)\)를 생각해보자. \(C(A)\)는 행렬의 랭크가 m이기에 n개의 (열)벡터 중 선형독립인 column vector는 m개 뿐이다. 따라서 벡터의 span인 열공간은 m차원 벡터공간이다. (n개의 열벡터가 존재하지만,선형종속이기떄문이다.)
위의 문제에서 A는 full row rank이다. 위해서 한 것처럼 먼저 \(C(A)\)와 \(b\)가 어떻게 위치하고 있을지 파악하고 null space를 따져 완전해를 구하는 것이다. 먼저 \(C(A)\)를 생각해보자. \(C(A)\)는 행렬의 랭크가 m이기에 n개의 (열)벡터 중 선형독립인 column vector는 m개 뿐이다. 따라서 벡터의 span인 열공간은 m차원 벡터공간이다. (n개의 열벡터가 존재하지만,선형종속이기떄문이다.)
이전문제와 다른점도 존재하는데 바로 열공간이 (열)벡터가 존재하는 벡터공간의 부분공간이 아니라는 점이다. 이 문제에서 각각의 열벡터는 m차원 공간의 벡터이고 열벡터의 생성도 m차원 벡터공간이기때문에 열벡터가 존재하는 바로 그 공간이 열공간이다.
위와 같이 열공간에 대해서 생각했으면 이제 b에 대해서 생각해볼 차례다. b의 위치는 어떻게 될까? b는 A의 열공간에 속하는 벡터일까 아닐까?
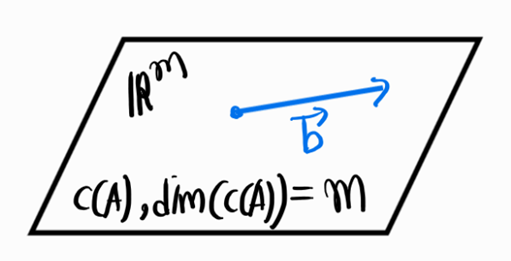
b의 경우 \(b \in \mathbb{R}^{m \times 1}\)이기에 열공간에 속하는 벡터이다. 그러므로 full row rank인 경우는 반드시 해가 존재한다.
여기서 완전해를 구하기 위해서 null space도 생각해야한다. 랭크-널리티 정리에 의해 다음과 같다.
랭크정리에 의해서 null space는 n-m차원의 벡터공간이다. 이 경우 가능한 \(x_{null}\)은 무한히 많이 존재하므로 해가 무수히 많다. 완전해는 다음과 같다.
\[\begin{aligned} \therefore\,\, &x_{complete} = x_{particular} + x_{null}\\ &\text{where, } x_{null} \in N(A) = \mathbb{R}^{n-m} \end{aligned}\]결론적으로, full row rank의 경우 해는 무수히 많다.
Case3 : A가 full rank일 때
문제 : \(A \in \mathbb{R}^{m \times m},\text{rank}(A) = m\,,x = \in \mathbb{R}^{n \times 1}\,,b\in \mathbb{R}^{m \times 1}\) 일때, \(Ax = b\)를 만족하는 x의 갯수는?
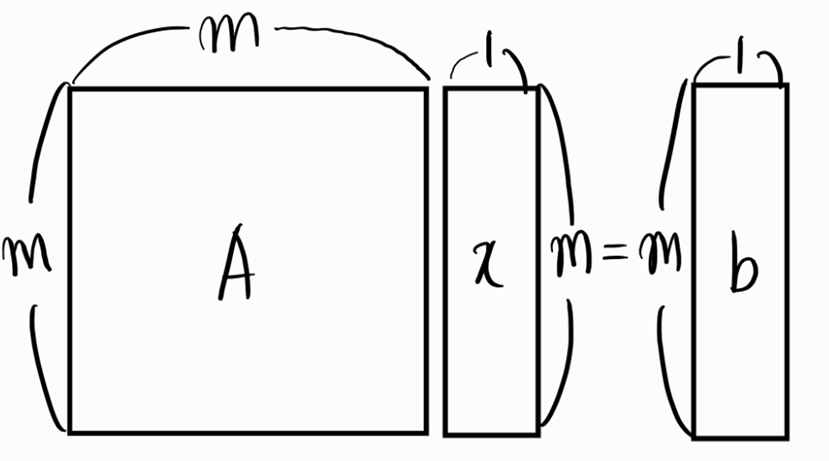
사실 이 문제의 해는 다음과 같다.
\[x = A^{-1}b\] 그러므로,full rank인 경우 해의 갯수가 1개이다.
위처럼 간단하게 해를 구할 수 있지만 … 그래도 기하학적으로 생각해보기 위에서 했던 것처럼 따져보자. column space는 m차원 벡터공간이다. column vector는 column space 그 자체인 m차원 벡터공간의 원소이다. \(b\in \mathbb{R}^{m \times 1}\)의 경우 m차원 벡터공간의 원소이다. 그러므로, column space는 반드시 b를 포함하며 그림으로 표현하면 다음과 같다.

널공간을 따지기 위해 랭크-널리티 정리를 사용해 보면 다음과 같다.
null space는 차원이 0이므로 \(N(A) = \{{\bf 0}\}\)이고 다음과 같다.
\[x_{complete} = x_{particular} + x_{null} = x_{particular} + {\bf 0} = x_{particular}\]
결과적으로, full rank인 경우 해는 반드시 존재하며 갯수는 1개이다.
Case4 : A가 rank deficient 일 때
문제 : \(A \in \mathbb{R}^{m \times n},\text{rank}(A) = \alpha < \text{min}(m,n)\,,x = \in \mathbb{R}^{n \times 1}\,,b\in \mathbb{R}^{m \times 1}\) 일때, \(Ax = b\)를 만족하는 x의 갯수는?

위의 예시에서는 A가 rank deficient인 경우 중, \(m<n\) 인 경우를 생각해보자. 행렬 A의 column space는 m차원 공간의 부분공간이자 \(\alpha\)차원의 벡터공간이다.\(b \in \mathbb{R}^{m \times 1}\)이므로 가능한 경우는 아래와 같다.
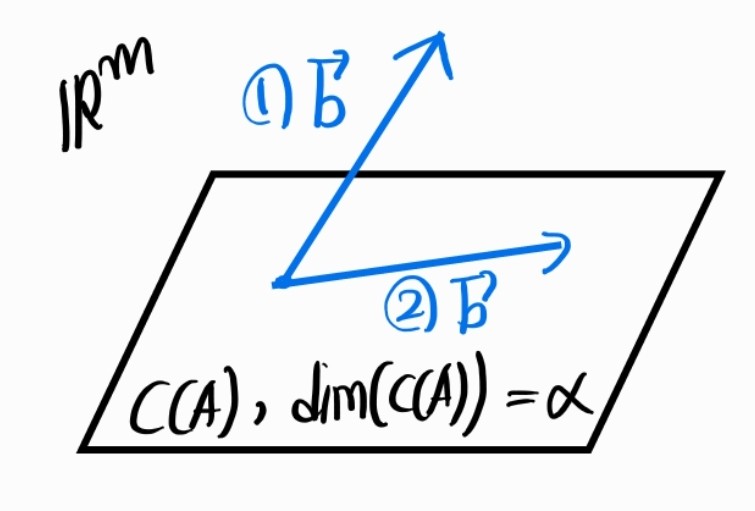
1번의 경우라면 b는 column space의 원소가 아니므로 방정식의 해는 존재하지 않는다. 만약 2번의 경우라면 해가 존재한다. 이때에는 null space를 고려한 완전해를 따져야하므로 랭크-널리티 정리를 확인한다.
랭크정리에 의해서 null space는 \(n - \alpha\)차원의 벡터공간이다. 이 경우 null space의 임의의 원소인 \(x_{null}\)는 무한히 많이 존재하므로 해가 무수히 많다. 완전해는 다음과 같다.
\[\begin{aligned} \therefore\,\, &x_{complete} = x_{particular} + x_{null}\\ &\text{where, } x_{null} \in N(A) = \mathbb{R}^{n-\alpha} \end{aligned}\]결론적으로, rank deficient의 경우 해는 무수히 많거나 해는 존재하지 않는다.
정리
| rank type | expression | 해의 갯수 |
|---|---|---|
| full column rank | \(A \in \mathbb{R}^{m \times n}\),\(\text{rank}(A) = n<m\) | 해가 없거나 해가 한개만 존재한다. |
| full row rank | \(A \in \mathbb{R}^{m \times n}\),\(\text{rank}(A) = m<n\) | 해가 무수히 많다. |
| full rank | \(A \in \mathbb{R}^{m \times m}\),\(\text{rank}(A) = m\) | 해가 한개만 존재한다. |
| rank deficient | \(A \in \mathbb{R}^{m \times n}\),\(\text{rank}(A) < \text{min}(m,n)\) | 해가 없거나 해가 무수히 많다. |