[Linear Algebra] 6-3.EVD of symmetric matrix

수튜브님의 직교대각화가능(orthogonal diagonalizability)을 보고 정리한 내용입니다.

사전지식

Orthonormal matrix

In linear algebra, an orthogonal matrix, or orthonormal matrix, is a real square matrix whose columns and rows are orthonormal vectors. (from wikipedia)

• 행벡터들과 열벡터들이 orthogonal(직교) + normal(크기가 1)인 정사각행렬을 orthonormal matrix라 한다.
• orthogonal matrix 또는 orthonormal matrix는 같은 표현이다.
• 그러나 직교 + 크기가 1인 벡터가 열벡터이기에 orthogonal + normal = orthonormal이 더 의미를 살리는 듯하여 여기서는 orthonormal matrix용어를 사용한다.

expression 1

• orthonormal matrix \(Q\)을 나타내는 첫 번째 표현은 아래와 같다.

\[\begin{aligned} &Q^TQ = QQ^T = I \\ &\text{where } I \text{ is the identity matrix} \end{aligned}\]

• 왜 저런 표현식이 나올까?
• 이는 정의를 함축하고 아주 잘 함축하고 있는 표현이다.
• 임의의 \(Q \in \mathbb{R}^{n \times n}\)가 다음과 같다고 해보자.

\[\begin{aligned} &Q = \begin{bmatrix} q_1 & q_2 & \dots q_n \end{bmatrix} \end{aligned}\]

• 여기서 \(q_i \in \mathbb{R}^{n \times 1}(i=1,2,\dots,n)\)은 \(Q\)의 column vector이다.
• 먼저 \(Q^TQ = I\)를 확인해보자.

\[\begin{aligned} Q^TQ = \begin{bmatrix} q_1^T \\ q_2^T \\ \vdots \\ q_n^T \end{bmatrix} \begin{bmatrix} q_1 & q_2 & \dots & q_n \end{bmatrix} = \begin{bmatrix} q_1^T,q_1 & q_1^Tq_2 & \dots & q_1^Tq_n \\ q_2^T,q_1 & q_2^Tq_2 & \dots & q_2^Tq_n \\ \vdots & \vdots & \vdots & \vdots \\ q_n^T,q_1 & q_n^Tq_2 & \dots & q_n^Tq_n\\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & \dots & 0\\ 0 & 1 & \dots & 0\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & 1\\ \end{bmatrix} \end{aligned}\]

• 좌우변이 같기때문에 아래가 유도된다.

\[\begin{aligned} q_i^Tq_j = \begin{cases} 1 \quad (i = j)\\ 0 \quad (\text{otherwise}) \end{cases} \text{for all }i \in (1,\dots,n),\,j \in (1,\dots,n) \end{aligned}\]

• 이는 같은 벡터끼리 내적을 하면 1이고 다른벡터끼리 내적하면 0임을 의미한다.
• 즉, 임의의 벡터\(q_i\)의 크기는 1인 unit vector이며 열벡터들은 orthogornal 하다는 것이다.

\[\begin{aligned} &\text{for all }i \in (1,...,n), j \in (1,...,n) \\ &|q_i| = \sqrt{q_i} = \sqrt{dot(q_i,q_i)} = 1 \\ &dot(q_i,q_j)=0 \longleftrightarrow q_i\perp q_j \end{aligned}\]

• 동일한 과정을 행벡터에 대해서도 수행하면 행벡터들도 orthonormal하다는 것을 보일 수 있다.

expression 2

• expression1으로부터 orthonormal matrix에 관한 다음의 식도 끌어낼 수 있다.

\[\begin{aligned} &Q^T = Q^{-1} \\ \end{aligned}\]

• 즉,어떤 행렬의 transpose가 그것의 inverse와 같으면 orthonormal matrix라는 것이며 이것또한 orthonormal matrix의 다른 표현이다.

• 왜 그런가 하면 expression1에서 \(Q^TQ = QQ^T = I\)였다. 그러므로 \(Q\)의 역행렬\(Q^{-1}\)는 \(Q^T\)와 같다.
  (Q의 역행렬은 \(Q^{-1}Q = QQ{-1} = I\)를 만족하는 행렬이다.)

orthogonally similar

• 다음과 같은 식을 만족하면 C는 A와 orthogonally similar(직교닮음)이다.

\[\begin{aligned} &C = Q^{-1}AQ \\ &\text{where } Q^{-1} = Q^T \end{aligned}\]

• 여기서 \(Q^{-1} = Q^T\)는 orthonomal matrix의 정의이다.
• 윗 식에 의해서 A도 C와 orthogonally similar임을 이끌어낼 수 있다.

\[\begin{aligned} &A = QCQ^{-1} \\ &\text{where } Q^{-1} = Q^T \end{aligned}\]

orthogonally diagonalize

• 임의의 정사각행렬 \(A,D\)에 대해서 다음이 만족한다고 해보자.

\[\begin{aligned} & \begin{aligned} D &= Q^{-1}AQ \\ &= Q^TAQ \\ \end{aligned} \\ &\text{where } D = diag(d_1,d_2,\dots,d_n) , Q^{-1} = Q^T \end{aligned}\]

• 이와 같이 \(A\)와 직교닮음인 대각행렬 \(D\)가 존재할때 행렬\(A\)가 직교대각화 되었다 라고 한다.

• 또한 이때 정사각행렬 \(A\)는 \(P^{-1}AP\)가 대각행렬\(D\)가 되게하는 가역행렬이자 orthornomal matrix인 \(P\)가 존재하기때문에 “행렬\(A\)는 orthogonally diagonalizable하다”라고 말한다.

• \(Q^T\)와 \(Q\)의 자리를 바꿔서 써도 된다. 즉 \(Q^{-1}\)를 새로운 Q로 본다면 다음과 같이 적을 수도 있다.

\[\begin{aligned} D &= QAQ^{-1}\\ &= QAQ^T\\ &\text{where } D = \text{diag}(d_1,d_2,\dots,d_n),Q^{-1} = Q^T \end{aligned}\]

• 단지 notation의 차이일 뿐이다. 역행렬의 관계이기 때문이다.

매우 중요한 정리
\(A\)가 대칭행렬이다 \(\Longleftrightarrow A\)가 orthogonally diagonalizable하다

• 위의 두 명제가 동치임을 보이기 위해 다음 두 정리를 증명한다.

명제1 : \(A\)가 orthogonally diagonalizable \(\rightarrow A = A^T\)

• 행렬\(A\)가 orthogonally diagonalizable하다고 하자. 즉 \(D = P^TAP\)를 만족하는 직교행렬 \(P\)가 존재한다. 이때 \(A^T\)를 전개하면 다음과 같다.

\[\begin{aligned} &A = PDP^{-1} = PDP^T\\ &A^T = (PDP^T)^T = PD^TP^T = PDP^T = A \end{aligned}\]

명제2 : \(A = A^T \rightarrow\) \(A\)는 orthogonally diagonalizable

• 수학적 귀납법으로 아래의 두 가지를 증명하면 된다.
  • \(A \in \mathbb{R}^{1 \times 1}\) 일때 직교대각화가 가능하다.(1)
  • \(A \in \mathbb{R}^{(n-1)\times (n-1)}\)때 직교대각화가 가능하다고 가정하고 \(A \in \mathbb{R}^{n \times n}\)때 직교대각화가 가능함을 보인다.(2)
  • 임의의 \(n\) 그리고 \(n-1\)에 대해서 성립함을 증명했고 1에대해서 증명했기 때문에 …

\[\begin{aligned} &\mathbb{R}^{1 \times 1} \rightarrow \mathbb{R}^{2 \times 2}\\ &\mathbb{R}^{2 \times 2} \rightarrow \mathbb{R}^{3 \times 3}\\ &\mathbb{R}^{3 \times 3} \rightarrow \mathbb{R}^{4 \times 4}\\ &\quad\quad\quad\vdots\\ &\mathbb{R}^{n-1 \times n-1} \rightarrow \mathbb{R}^{n \times n}\\ &\quad\quad\quad\vdots\\ \end{aligned}\]

• 이렇게 증명하면 모든 \(n\) 결국은 모든 대각행렬에 대해서 직교대각화가 가능함을 보일 수 있다.
• 느낌
  • 하나의 증명을 위해서 모든 자연수에 대해 딸려있는 증명들을 해야되네?! \(\rightarrow\) 작은 것부터 차례차례 쓰러뜨려보자! \(\rightarrow\) 작은거 하나하나 다하기 힘드니까 임의의 n에 대해서 해보자.!
  • (1)을 증명하고 (2)만 증명하면 모든 n에 대해서 증명할 수 있어서 (2)를 증명해서 뚫는 느낌.
  • 도미노 : 하나를 쓰러뜨리면 그 다음이 쓰러지는 것을 알고있어(증명했어). 증명해야 될 문제는 맨 처음부터 맨 마지막까지 전부 쓰러뜨리면 되는문제야. 맨 처음이 무너진다면 다음에 오는 모든 것들이 무너질꺼야.

먼저 \(A \in \mathbb{R}^{1 \times 1}\) 일때 직교대각화가 가능함을 보인다. 먼저 \(A\)와 \(P\)행렬을 잡는다.

\[\begin{aligned} &A = \begin{bmatrix}a\end{bmatrix} \in \mathbb{R}^{1 \times 1} \\ &P = \begin{bmatrix}1\end{bmatrix} \in \mathbb{R}^{1 \times 1} \end{aligned}\]

여기서 \(A=A^T\)인 대칭행렬이며 \(P\)의 경우 \(P^{-1} = P^T\)가 성립하는 orthonomal matrix이다.

\[\begin{aligned} D = P^{-1}AP = \begin{bmatrix}a\end{bmatrix} \end{aligned}\]

D는 대각행렬이다. 따라서 \(D = P^{-1}AP\)를 만족하는 가역행렬이자 직교행렬인\(P\)와 대각행렬\(D\)가 존재하므로 행렬\(A \in \mathbb{R}^{1 \times 1}\)는 orthogonally diagonalizable하다.

• D는 대각행렬이다. 따라서 \(D = P^-1AP\)를 만족하는 가역행렬이자 직교행렬인\(P\)와 대각행렬\(D\)가 존재하므로 행렬\(A \in \mathbb{R}^{1 \times 1}\)는 orthogonally diagonalizable하다.
• 정리2 자세한 증명 생략…
• 따라서 어떤 행렬이 대칭행렬 \(\Longleftrightarrow\)직교대각화가 가능하다.

EVD of symmetric matrix

• Symmetric matrix \(A = A^T \in \mathbb{R}^{n \times n}\)의 경우의 EVD는 조금 특별하다.

\[\begin{aligned} &A = V\Lambda V^{-1}\\ &A^T = V^{-T}\Lambda^T V^{T} = V^{-T}\Lambda V^{T} \end{aligned}\]

• 위와 같이 전개가 된다.
• 여기서 \(A = A^T\)임을 사용하면…

\[\begin{aligned} &A = A^T\\ &\Longrightarrow V\Lambda V^{-1} = V^{-T}\Lambda V^{T} \end{aligned}\]

• 윗 식을 만족하는 \(V\)는 \(V^{-1} = V^T\)인 orthonormal matrix이다.
  • 엄밀하게는 \(V\)는 \(V^{-1} = V^T\) orthonormal matrix가 될 수 있다가 맞는 것 같다.
  • 느낌상 맨위의 표현으로 기억하고 익숙하다면 좀 더 세부적으로 기억해보자.
  • 예시 : 반드시 직교대각화만 되는 건 아니다?!링크넣기,orthogonally diagonolizable 참고
• 이는 무엇을 의미할까? \(\to V^{-1}\)를 찾는 번거로움이 줄어든다.
  • 원래의 EVD라면 \(V\)를 구하고 \(V^{-1}\)를 따로 구해줘야 한다.(역행렬 구하는 것이 쉽지많은 않을 것이다.특히 차원이 커질수록!)
  • Symmetric하다면 \(V\)를 구하고 transpose만 취해주면 된다.
• 즉 Symmetric하다면 고윳값분해는 다음과 같다.

\[A = V\Lambda V^{-1} = V \Lambda V^T\]

• orthonormal matrix를 보통 Q로 많이 적으므로 여기서부터는 \(V\)를 \(Q\)로 적겠다.

Symmetric matrix의 EVD와 orthogonally diagonalizable의 연관성

• 잠깐 넘어가기 전에 중요한 중요한 사실 하나를 짚고 넘어가자.
• 우리는 정리를 통해서 Symmetric matrix는 직교대각화가 가능하다는 사실을 알고 있다.
• 하지만 이러한 사실만 알고있을뿐 실제로 어떻게 \(P\)와 \(D\)를 구하는지는 알지 못했다.
• 대칭행렬의 경우 직교대각화는 EVD를 통해 구현할 수 있다. 이는 정방행렬의 경우와 유사하다.(정방행렬의 EVD와 orthogonally diagonalizable 참고)
  • 정방행렬의 경우 대각화는 EVD를 통해서 구현할 수 있었다.
  • 대칭행렬의 경우 직교대각화는 EVD에서 \(V^{-1} = V^T\)인 V가 구해지기에 구현할 수 있다.

신기하고 중요한 사실들

신기한 사실1 : 대칭행렬 A는 rank1 매트릭스들의 가중합으로 표현할 수 있다.

• EVD를 계속해서 전개해보면 다음과 같다.

\[\begin{aligned} A &= V\Lambda V^T = \begin{bmatrix} q_1 & q_2 & q_3 \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 & 0 \\ 0 & \lambda_2 & 0 \\ 0 & 0 & \lambda_3\\ \end{bmatrix} \begin{bmatrix} q_1^T \\ q_2^T \\ q_3^T \end{bmatrix} = &\begin{bmatrix} \lambda_1q_1 & \lambda_2q_2 & \lambda_3q_3 \end{bmatrix} \begin{bmatrix} q_1^T \\ q_2^T \\ q_3^T \end{bmatrix}\\ &= \lambda_1q_1q_1^T + \lambda_2q_2q_2^T + \lambda_3q_3q_3^T = \sum_{i=1}^3 \lambda_iq_iq_i^T \end{aligned}\]

• 여기서부터 재미난 사실을 알 수 있다.

• \(q_iq_i^T\)는 rank가 1인 matrix이다.

• 마지막 수식은 이러한 rank-1 matrix들을 적절하게 상수배하고 더하여 합을 취하면 \(A\)가 나온다는 것이다. 상수가 각각에 대응하는 rank-1 matrix \(q_iq_i^T\)의 중요도,기여도를 고려한 가중치라고 생각한다면?

• 다음과 같은 해석을 할 수 있다.

  • 어떤 정방행렬\(A\)는 여러개의 rank-1 matrix들이 섞인거야.
  • 그런데 그냥 섞인건 아니고 중요한건 많이 안중요한건 적게 섞은 것이 정방행렬이야!
  • 그때의 중요도는 \(\lambda_i\)가 알려줘.

• 그림으로 보면 이런느낌이다.! 그림

• 만약에 데이터의 크기가 너무 커서 압축을 해야하는 상황이라면 이를 응용할 수 있다.

  • 이미지의 크기가 너무크다. 조금 사이즈를 줄이고 싶다.
  • 중요도 \(\lambda_i\)가 상대적으로 작은 matrix들은 조금 제외를 해도 괜찮겠지?
  • 실제로 된다. 조금 줄여도 여전히 인식할 수 있는 정도이다.(조금 화질이 안좋아지긴 한다.)

신기한 사실2 : 선형변환이 대칭행렬이라면 입력벡터는 직교하는 고유벡터로 분해하고 적절하게 줄이고 늘려서 재조합한 된다.

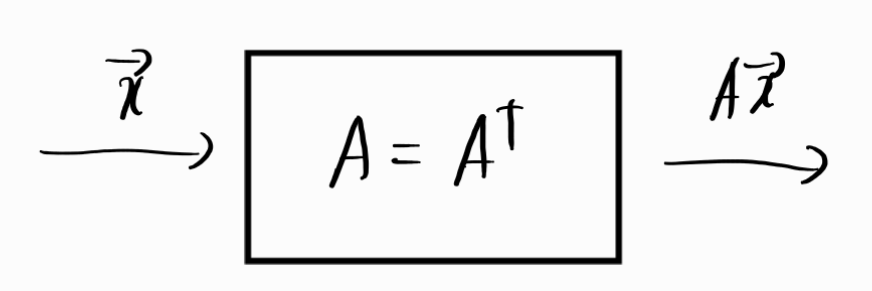
• 위의 그림과 같이 선형변환이 Symmetric matrix \(A = A^T\)인 경우를 고려해보자.
• \(A\)를 EVD하고 rank-1 matrix의 가중합으로 표현했을때 \(x\)에 대한 선형변환 \(Ax\)는 다음과 같다.

\[Ax = \lambda_1q_1q_1^Tx + \lambda_2q_2q_2^Tx + \lambda_3q_3q_3^Tx\]

• \(x \in \mathbb{R}^3\)에 대하여 \(q_i^Tx\)는 각각의 직교하는 3차원 공간의 또다른 정규직교기저에 대한 \(x\)의 성분을 의미한다.
• \(q_i(i=1,2,3)\)로 표현된 \(x\)는 다음과 같다.

\[\begin{aligned} x = (q_1^Tx)q_1 + (q_2^Tx)q_2 + (q_3^Tx)q_3 = \begin{bmatrix}q_1^Tx \\ q_2^Tx \\ q_3^Tx\end{bmatrix} \end{aligned}\]

• 간단하게 말해서 \(q_1,q_2,q_3\)를 포함하도록 \(x\)를 분해했다고 보면된다.

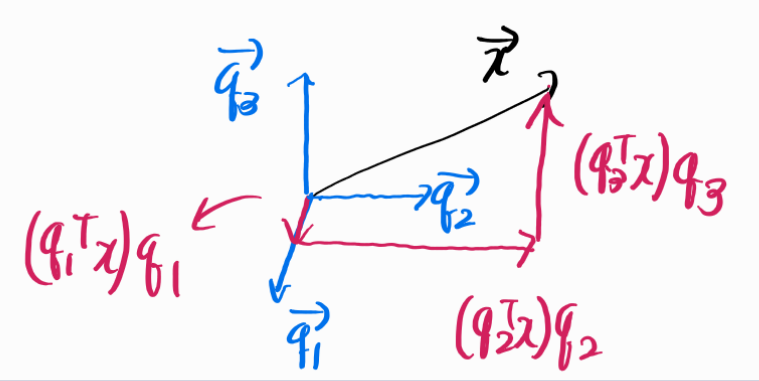
• 그럼 \(Ax\)는?? \(\to Ax\)는 직교기저로 \(x\)를 분해하고 각 성분에 대해 적절한 스칼라배를 취해서 다시 조합하여 섞은 것으로 이해할 수 있다.
  • 첫번째 성분인 \((q_1^Tx)q_1\)은 \(\lambda_1\)만큼 곱한다. \(\to \lambda_1q_1q_1^Tx\)
  • 두번째 성분인 \((q_2^Tx)q_2\)은 \(\lambda_2\)만큼 곱한다. \(\to \lambda_2q_2q_2^Tx\)
  • 세번째 성분인 \((q_3^Tx)q_3\)은 \(\lambda_3\)만큼 곱한다. \(\to \lambda_3q_3q_3^Tx\)
  • 곱한것들을 +해서 섞으면 \(x\)를 대칭행렬로 선형변환한 \(Ax\)이다.
• 즉, \(Ax = \lambda_1q_1q_1^Tx + \lambda_2q_2q_2^Tx + \lambda_3q_3q_3^Tx\)이다.

정리

• Symmetric matrix의 경우 EVD가 조금 더 간단하다.
  • 이는 \(V^{-1} = V^T\)로 구해지기 때문이다.
• 또한 재밌는 사실도 두 가지 나왔다.
  • Symmetric matrix는 rank-1 matrix의 가중합이다. \(\to\) 데이터 압축,축소,PCA 응용(1)
  • Symmetric matrix가 선형변환이라면 그러한 선형변환은 Input을 직교기저로 분해하고 적절히 스칼라배하여 재조합 한 것이다.(2)
• 특히(1)의 경우는 유용할 것 같지만 여기서는 Symmetric matrix로 하는 방법만 배웠다.
• SVD의 경우 일반적인 행렬에 대해서 할 수 있다.(만능)

참고자료

수튜브
공돌이의 수학정리노트
혁펜하임 선형대수학 5-2강. 고윳값 분해 (Eigendecomposition) 의 모든 것!