-2.925Reward
리워드의 정의는 다음과 같다.
\[\mathcal{R}_{t+1} \overset{\Delta}{=} \mathbb{E}({R}_{t+1}|S_t=s,A_t=a)\]
이는 \(s_t\)에서 \(a_t\)를 했을때 t+1에서 얻는 값을 나타내는 확률변수\(R_{t+1}\)의 기댓값이다.이다.
알파고를 예를 들어서 생각해보자. 알파고가 바둑판에(\(s_t\))에 검은돌을 놓으면(\(a_{t}\)) 상대하는 사람(또는기계)도 어떤 위치에 흰돌을 놓을것이다. 이 흰돌의 위치는 random이기 때문에 따라서 알파고가 확률변수 \(R_{t+1}\)이 존재하며 그것의 평균값을 리워드\(\mathcal{R}_{t+1}\)로 정의한다.
생각해보면 리워드는 뭔가 \(s_t\)에서 \(a_t\)를 해서 변하는 상황 \(s_{t+1}\)에 부여되는게 맞을 것 같다.찾아보니 위키피디아에는 reward를 \(R_a(s,s')\)로 쓴다. 변하는 상황에 따라 부여되는것도 맞고 어떤 액션을 취하면 그것에 상응한다고 봐도 무방할 것 같다.(개인적인 의견입니다.)
그냥 \(R_{t+1}\)을 리워드라 하는 경우도 많은 것 같다
위에서 인식하는 상황이라고 썼는데 사실 state는 agent가 인식하는 것이 아니라 사실은 environment에가 반환(return)하는 것입니다. agent는 state중 일부를 받는데 이것을 observation이라고 합니다. 그러나 실제 논문에서는 딱히 state와 observation을 구별하지않고 쓰는 경우가 많다고 합니다.
Return
\[\begin{aligned} &\text{definition of return } G_t\\ &G_t \overset{\Delta}{=} R_t + \gamma R_{t+1} + \gamma R_{t+2} + \dots \end{aligned}\]return(\(G_t\))은 현재에서 부터 시작하여 앞으로 받게될 미래의(discounted) reward들의 total sum이다. 강화학습의 목적은 return의 평균(기댓값)을 가장 크게 만드는 policy들을 찾는 것이다. 조금 풀어쓰자면 강화학습은 agent의 지금 당장의 reward와 미래의 reward를 염두하여 취해야할 action에 대한 policy을 학습하는 것이다.
Discount factor
\[\text{discount factor } \gamma \in [0,1]\]
discount factor(\(\gamma\))는 return에서 reward곱해지는 값이다. 이 값이 작을수록 지금 당장리워드를 받는것에 집중하고(근시안적인 사고) 이 값이 클수록 미래에 받는 리워드를 중요하게 생각(미래지향적)한다. 또한 효율적인 path결정을 위해서도 중요하다.
또한 크기가 무한히 커질때 크기비교를 못하므로 수학적으로 문제가 된다고 한다.
value function
state value function
- The value function of a state \(s\) under a policy \(\pi\) is the expected return when starting \(s\) and following \(\pi\) thereafter.
\(\leftrightarrow\) policy \(\pi\)를 따를때 state \(s\)의 value function은 state \(s\)에서 시작하여 그 후 \(\pi\)를 따를때 return의 기댓값이다. - 각각의 상태가 얼마나 좋은지 그 가치를 expected return으로 계산한 함수이므로 state value function이라는 이름이 붙었다.
- 단,\(s\)에서 시작하다는 조건하에서의 기댓값이므로 \(s\)가 given인 conditional expectation을 구하면 된다.
\[v_{\pi}\overset{\Delta}{=} \mathbb{E}_{\pi}[G_t|S_t=s] = \mathbb{E_{\pi}}\left[{\sum_{k=0}^{\infty}\gamma^kR_{t+k+1}|S_t=s}\right],\text{for all s } \in S\]
action value function
- Similary, we define the value of taking action \(a\) in state \(s\) under a policy \(\pi\) as the expected return starting from s,taking action a,and thereafter following policy \(\pi\)
\(\leftrightarrow\) 유사하게 policy \(\pi\)를 따르고 state \(s\)에서 action \(a\)를 취하는 것의 가치는 state \(s\)에서 시작하여 action \(a\)를 취하고 그 후 \(\pi\)를 따를때의 기댓값으로 정의할 수 있다. - 각각의 state에서 action을 취했을때 그 가치를 expected return으로 측정하므로 action value function이라는 이름이 붙었다.
- 여기서는 state s에서 action a를 취한것에 대한 기댓값을 계산하므로 given s,a일때의 conditional expectation of return을 구하면 된다.
\[q_{\pi}(s,a) \overset{\Delta}{=} \mathbb{E}[G_t|S_t = s,A_t = a] = \mathbb{E}_{\pi}\left[\sum_{k=0}^{\infty}\gamma^kR_{t+k+1}|S_t=s,A_t=a\right]\]
recursive relationships
v를 next v로 표현하기
- For any policy \(\pi\) and any state \(s\), the following consistency condition holds between the value of \(s\) and the value of its possible succesor states
\(\leftrightarrow\) 상태 \(s\)의 state value function은 다음 상태 \(s'\)에 대한 state value function이 포함된 식으로 표현할 수 있다.즉,현재상태의 가치는 다음상태의 가치와 연관과 관련이 있다.
\[\begin{align} v_{\pi}(s) &\overset{\Delta}{=} \mathbb{E}_{\pi}[G_t|S_t=s] \\ &=\mathbb{E}_{\pi}[R_{t+1}+\gamma G_{t+1}|S_t=s] \\ &=\sum_a \pi(a|s)\sum_{s'}\sum_{r}p(s',r|s,a)\left[r + \gamma E_{\pi}[G_{t+1}|S_{t+1}=s'\right]]\\ &=\sum_a \pi(a|s)\sum_{s',r}p(s',r|s,a)\left[r + \gamma v_{\pi}(s')\right] , \text{for all } s \in S\\ \end{align}\]
혹시 2에서 3번식으로 넘어가는게 이해가 잘 안된다면 링크를 참고. 핵심은 law of total expectation을 이해하는 것이다.
이 식이 기억하기가 상당히 어렵다. 따라서 \(s \rightarrow s'\)을 나타낸 \(v_{\pi}\)의 backup diagram을 통해서 생각해볼 수 있다.
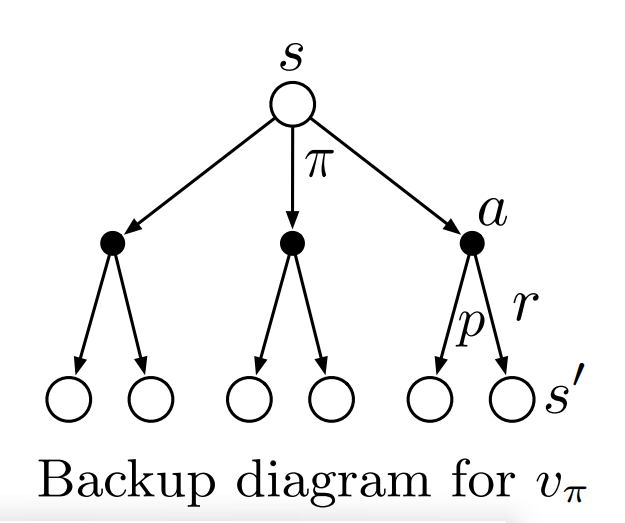
- 각각의 흰색원은 state를 검은색원은 state,action pair를 나타낸다.
- 상태s에서 시작하며 policy \(\pi\)에 의하여 action을 취한다.
- action을 취하면 리워드\(r\)을 얻고 \(s \rightarrow s'\)으로 상태가 바뀌며 이는 transition \(p(s',r|s,a)\)에 의해 결정된다.
The Bellman equation (3.14) averages over all the possibilities, weighting each by its probability of occurring. It states that the value of the start state must equal the (discounted) value of the expected next state, plus the reward expected along the way.
\(\leftrightarrow\)즉, 초기상태 \(s\)에서 시작하여 나올 수 있는 모든 \(r,v_{\pi'}\)의 경우에 대해 각각이 나올 확률을 곱하여 averaging(expectation)을 구하면 \(v_{\pi}(s)\)라는 것이다.
\[\begin{align} v_{\pi}(s) &= \sum_{a,s',r}\pi(a|s)p(s',r|s,a)\left[r + \gamma v_{\pi}(s')\right] , \\ &= \sum_{a}\pi(a|s) \sum_{s',r}(s',r|s,a)\left[r+\gamma v_{\pi}(s')\right] \,\text{for all } s \in S\\ \end{align}\]
개인적으로 좀 더 자세히 기억하려고 정리해봤다.diagram은 수식자체는 아니기 때문에 그림을 보고 나름대로 기억할 수 있는 방법을 찾으면 된다고 생각한다. 따라서 아래와 같이 정리해봤지만 헷갈리면 pass해도 무방하다.
- \(s \rightarrow s'\)는 여러가지 경우가 존재하며 그러므로 상태 \(s\)의 가치 \(v_{\pi}(s)\)는 다음상태 \(s'\)의 가치 \(v_{\pi}(s')\)에 영향을 받는다.
- 그런데 \(s'\)은 \(r\)이 항상 같이 따라오므로 \(v_{\pi}(s)\)는 \(r+v_{\pi}(s')\)에 영향을 받는다.
- 상태s에서 a를 취하며 \(r\)과 \(s'\)이 나올 확률은 policy와 transition의 곱이다. 즉 \(\pi(a|s)p(s',r|s,a)\)이다.
- 모든 경우에 대해 고려해야 하므로 모든 \(a,r,s'\)에 곱해준다.
Q를 next Q로 표현하기
- 마찬가지로 \(s,a\)에서의 action value function도 next \(s',a'\)에서의 action value function으로 표현할 수 있다.
\[\begin{align} q_{\pi}(s,a) &\overset{\Delta}{=} \mathbb{E}_{\pi}[G_t|S_t=s,A_t=a] \\ &=\mathbb{E}_{\pi}[R_{t+1}+\gamma G_{t+1}|S_t=s,A_t=a] \\ &=\sum_{s',r}p(s',r|s,a)\big[r+\sum_{a'}p(s',r|s,a)\pi(a'|s')q_{\pi}(a',s')] \end{align}\]
- backup diagram은 다음과 같다.
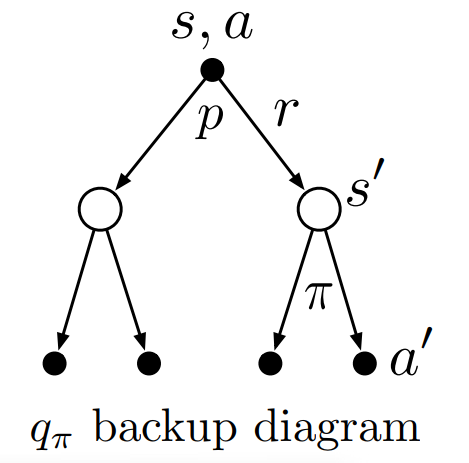
- backup diagram을 보고 나올 수 있는 \(r,q_{\pi}(s',a')\)의 모든 경우에 대하여 계산해보면 다음과 같다.(state value function의 \(r,s'\)은 같이 따라오므로 같이 계산해줬지만 action value function은 \(r,a\)는 따로이므로 따로 계산하여 더해준다.)
optimal policy
optimal policy는 value function인 \(V(s_t)\)를 가장 크게 하는 policy들(\(p(a_t|s_t),p(a_{t+1}|s_{t+1}),\dots,p(a_{\infty}|s_{\infty})\))이다.나중에 더 자세히 공부해야할 것 같다.
action value function은 state,action의 함수의 입력으로 주어지는 어떤 state에서 (마찬가지로 주어지는)action을 취했을때 특정 policy가 좋은지 나쁜지(가치)를 평가한다. 평가는 action을 취한뒤의 다음 state부터 마지막 시점까지 Agent가 가능한 모든 action과 놓여질 수 있는 모든 state를 고려하여 기대되는 보수의 총합을 계산하는방식이다. 이것도 마찬가지로 결국은 \(G_t\)에 대한 조건부 함수이다.
\[\begin{aligned} Q^{\pi}(s_t,a_t) \underset{=}{\Delta} \mathbb{E}[G_t|A_t=a_t,S_t=s_t,\pi] = \int_{s_{t+1}:a_{\infty}}G_tp(s_{t+1},\dots,a_{\infty})ds_{t+1}:da_{\infty} \end{aligned}\] \[\begin{aligned} \end{aligned}\] \[\begin{aligned} v_{\pi} \end{aligned}\]