<matplotlib.legend.Legend at 0x1f25fe4e730>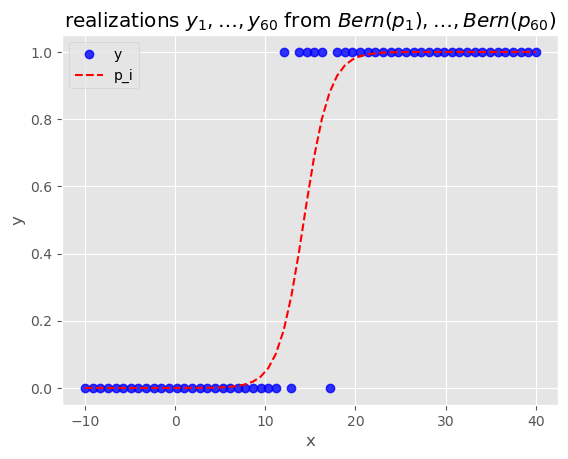
신호연
December 26, 2022
로지스틱회귀에 대해서 정리한 글입니다.
로지스틱회귀는 이진분류문제를 풀기위한 모형이며 종속변수 Y는 범주형 변수로 2가지 값 0또는 1만을 가질 수 있습니다. 파라미터를 사용하여 종속변수 y값을 설명한다는 점에서 선형회귀와 비슷하지만 y가 범주형변수라는 점과 분류문제에 사용되는 모델이라는 차이점이 있습니다.
로지스틱회귀의 기본 가정은 다음과 같습니다.
- 각각의 데이터요소(샘플)는 여러개의 독립변수와 0또는1만 가질수 있는 종속변수로 이루어져 있습니다.
- 임의의 m개의 독립변수와 이진 종속변수를 가지는 i번째 샘플을 나타나면 다음과 같습니다.\(x_{m,i}\)는 임의의 i번째 관측치의 m번째 변수를 의미합니다
\[(x_{1,i},x_{2,i},\dots,x_{m,i}),Y_{i} \]
- \(x_{1,i},x_{2,i},\dots,x_{m,i}\)가 주어질 때, 종속변수 \(Y_{i}\)는 베르누이 분포를 따르는 확률변수입니다.
- 확률변수\(Y_{i}\)가 따르는 확률함수를 구체적으로 표현한 식입니다.
\[Pr\,(Y_{i} = y|x_{1,i},x_{2,i},\dots,x_{m,i}\,) =
\begin{cases}
p_i & \text{if }y=1, \\
1-p_i & \text{if }y=0
\end{cases} = p_i^y(1-p_i)^{1-y}\]
- 기댓값은 실험 또는 시행을 무한히 반복했을때 확률변수가 취하는 값의 평균으로 기대되는(expected) 값(value)입니다. 베르누이분포를 따르는 확률변수 \(Y_{i}\)의 기댓값을 구하면 다음과 같습니다.
\[E\,[Y|x_{1,i},x_{2,i},\dots,x_{m,i}]\, = \sum_{i=0}^{i=1}p_iy = 1 \times p_{i} + 0 \times (1-p_{i}) = p_{i}\]
<matplotlib.legend.Legend at 0x1f25fe4e730>
기댓값은 실험 또는 시행을 무한히 반복했을때 확률변수가 취하는 값의 평균으로(또는 샘플링된 값의 평균) 기대되는 값입니다. 확률변수가 베르누이 분포를 따르는 경우 확률변수에 대한 기댓값(\(E\,[y|x_{1,i},x_{2,i}\.,\dots,x_{m,i}]\))과 모수\((p_i)\)가 같은 값을 가집니다. 그러므로,만약에 주어진 샘플데이터로부터 베르누이분포의 모수를 적절히 추정할 수 있다면 주어진 조건하에서 실험 또는 시행을 무한히 반복할 경우 확률변수가 1인사건과 0인사건중 어떤 사건이 더 많이 발생할지 알 수 있고 이를 바탕으로 종속변수 Y의 값을 결정하는 것은 타당합니다.
- e.g.
선형회귀에서 추정하고자하는 변수\(y\)는 \(x_0,x_1,...,x_m\)과 \(w_0,w_1,...,w_m\)과의 linear combination이였습니다.위에서 언급했듯이 특정샘플에 대한 모수를 적절하게 추정할 수 있다면 관측치가 어떤 클래스에 속할지 합리적으로 알 수 있으므로,로지스틱회귀에서도 선형회귀에서의 아이디어를 핵심아이디어를 가지고와서 추정하고자 하는 모수\(p_i\)를 \(x_0,x_1,...,x_m\)과 \(w_0,w_1,...,w_m\)의 linear combination로 표현하고자 합니다.
선형회귀의 아이디어(linear combination) + 모수에 대한 표현이라는 조건을 만족하기 위해서 최종적인 식은 다음과 조건을 만족해야 것입니다.
- \((x_0,x_1,...,x_m)\,,(w_0,w_1,..,w_m)\)의 linear combination 식에 있어야 함.
- linearcombination = 모수(추정하고자하는값)여야 함.
why linear combination?
위 식을 해석하기 위해 \(X\)의 첫번째 요소인 \(x_1\)에 대응하는 회귀계수 \(w_1\)이 학습결과 3으로 정해졌다고 가정해봅시다.만약 \(x_1\)의 값이 1증가한다면 로그오즈비가 3증가합니다.
최종적으로, 앞서 목적이었던 X와 W의 선형조합이 수식내부에 존재하도록 새롭게 표현한 모수는 다음과 같습니다. \[p_i(y) = Pr\,(y = 1|X_i;W)\, = \frac{1}{\,1 + e^{-WX_i}\,}\]
베르누이분포의 모수 \(p_i\)가 새롭게 표현되었으므로 확률질량함수도 새롭게 표현할 수 있습니다. 마지막 수식은 베르누이 분포의 확률질량함수가 모수\(W\)에 관한 식으로 바뀌었음을 표현합니다.
\[\begin{align}
Bern(y;p_i) = Pr\,(Y_{i} = y|x_{1,i},x_{2,i},\dots,x_{m,i};p_i) &=
\begin{cases}
p_i & \text{if}\,y=1 \\
1-p_i & \text{if}\,y=0
\end{cases} \\
&= p_i^{y}(1-p_i)^{1-y} \\
&= \frac{e^{yWX_i}}{1+e^{WX_i}}
\end{align}\]
베르누이 분포의 모수 \(W\)만 적절하게 추정할 수 있다면 임의의 데이터에 대해서 독립변수 \(X_i = (x_{0,i},x_{1,i},\dots,x_{m,i})\)가 들어왔을때 \(p_i = Pr(Y=1|X_i;w)\)를 구하고 샘플이 속하는 적절한 클래스(0 또는 1)을 예측할 수 있습니다. 베르누이 분포의 모수는 어떻게 추정할 수 있을까요?
주어진 상황은 다음과 같습니다.
MLE를 통해 모수를 추정합니다.(참고:MLE)
가능도는 다음과 같습니다.
\[L(W;y_1,y_2,\dots,y_n) = p_{Y_1,Y_2,\dots,Y_n}(y_1,y_2,\dots,y_n;W) = \underset{i=1}{\overset{i=n}{\large{\prod}}}\frac{e^{y_iWX_i}}{1+e^{WX_i}}\]
목적함수가 최솟값을 가지려면 \(\large{\frac{\partial J}{\partial w_0}=\frac{\partial J}{\partial w_1}=\frac{\partial J}{\partial w_2}=\dots\ = \frac{\partial J}{\partial w_m}} = 0\)
즉,\(\nabla_wJ(W) = [\large{\frac{\partial J}{\partial w_0},\frac{\partial J}{\partial w_1},\frac{\partial J}{\partial w_2}=\dots\,\frac{\partial J}{\partial w_m}}]^\text{T} = \overrightarrow{\bf{0}}\) 이어야 합니다. 목적함수를 임의의 \(w_k\)편미분하여 0이 되는 방정식은 다음과 같습니다
위와 같이 m개의 변수에 대해서 미분하면 m개의 방정식이 존재합니다. 그러나 정리하여 풀어낼 수 없는형태이므로 닫힌형태(closed-form)로 해가 존재하지 않습니다.
위에서 해석적으로 logstic regression의 해를 구할 수 없기때문에 다른 방법들을 써야합니다. 여기서는 경사하강법으로 해를 구합니다. 경사하강법을 사용하기 위해서 NLL을 베르누이분포의 2번식을 활용하여 전개하면 다음과 같습니다. 이번에는 베르누이 분포의 모수를 \(p_i\)로 놓고 진행했습니다.
\[NLL = -\sum_{i=1}^{n}y_i\text{ln}\,p_i(1-y_i)\text{ln}\,(1-p_i)\]
우리의 목적은 다음과 같습니다.이번에는 모수가 \(p_i\)인 베르누이 분포였으므로 추정량도\(\hat{p_i}\)입니다.
\[\hat{p_i} = \underset{p_i}{\text{argmin}}-\sum_{i=1}^{n}y_i\text{ln}\,p_i(1-y_i)\text{ln}\,(1-p_i)\]
위식에 대해서 직접 계산은 해보지 않았지만, 해석적으로 해를 구할 수 없음을 알았습니다. 그러므로 경사하강법을 이용해서 해를 구합니다. 최솟값을 찾고자 하는 Loss function은 다음과 같이 쓸 수 있습니다.Binary Cross Entropy와 같은 수식입니다.
\[L(\hat{y_i}) = -\sum_{i=1}^{n}y_i\text{ln}\,\hat{y_i}+(1-y_i)\text{ln}\,(1-\hat{y_i})\]
약간의 notation 변경이 있습니다.로지스틱회귀의 likelyhood를 최대화(또는 최소화)하여 나온 estimated value(추정치)는 \(\hat{p_i}\) = \(\hat{y_i}\)입니다. 경사하강법은 NLL에서 모수 \(p_i\)에 대한 추정치\(\hat{p_i}\)를 계속해서 대입해보고 틀린지 파악하고 반복적으로 추정치를 업데이트 합니다. 그러므로, \(p_i\) 대신 \(\hat{p_i}\)를 쓰는 것으로 보입니다.
로지스틱회귀의 적합을 pytorch를 사용하여 구현. Gradient Descent 활용
torch.manual_seed(2022)
n=400
#1 모수 W가정
W = torch.tensor(
[[-0.8467],
[0.041]]).float()
#2 각각의 관측치(데이터요소)에서의 모수 p_i시각화(시그모이드 함수 시각화)
_x = torch.linspace(-150,150,n).reshape(-1,1)
_one = torch.ones((n,1))
X = torch.concat((_one,_x),axis=1)
p_i = sig(X@W)
y = torch.bernoulli(p_i)
plt.xlim([-150,150])
plt.plot(X[:,1],y,"bo",alpha=0.5)
plt.plot(X[:,1],p_i,"r--")
plt.xlabel("x")
plt.ylabel("y,$p_i$")
plt.title("realizations $y_1,\dots,y_{300}$ from $Bern(p_1),\dots,Bern(p_{300})$")
plt.legend(["y","p"])<matplotlib.legend.Legend at 0x1f2684bfe20>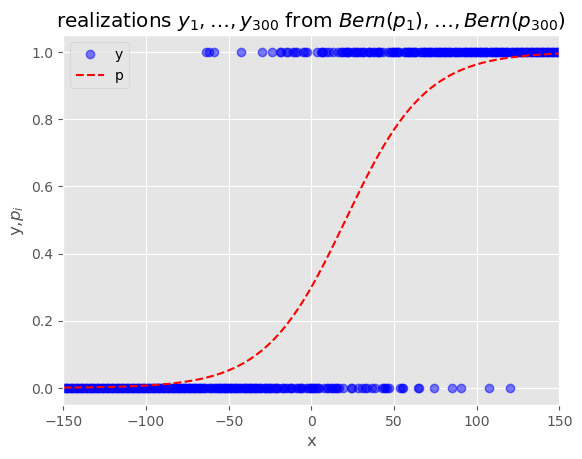
import torch
import matplotlib.pyplot as plt
plt.style.use('ggplot')
torch.manual_seed(2022)
n=400
#2 임의의 W에 대한 estimated value(추정치) What 초기화
What = torch.tensor(
[[0.],
[-0.03]],requires_grad=True)
_x = torch.linspace(-150,150,n).reshape(-1,1)
_one = torch.ones((n,1))
X = torch.concat((_one,_x),axis=1)
yhat = sig(X@What)
plt.plot(X[:,1].data,y,"bo",alpha=0.3)
plt.plot(X[:,1].data,p_i,"r")
plt.plot(X[:,1].data,yhat.data,"g")
plt.xlabel("x")
plt.ylabel("y")
plt.title("realizations $y_1,\dots,y_{60}$ from $Bern(p_1),\dots,Bern(p_{60})$")
plt.legend(["y","$p_i$","$\hat{y}(\hat{p_i})$"])<matplotlib.legend.Legend at 0x1f268e11e50>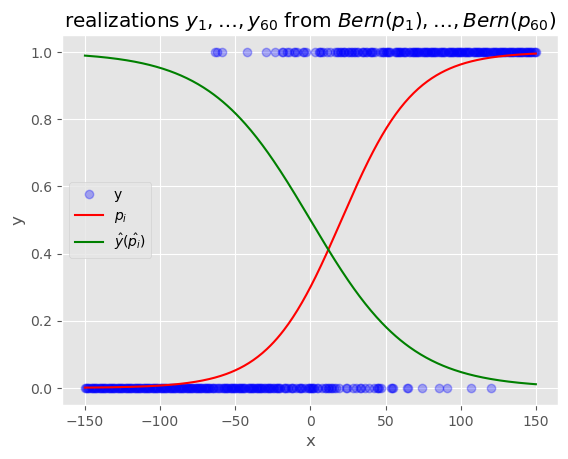
loss_fn = torch.nn.BCELoss()
"""
def BCE_Loss(yhat,y):
return torch.mean(y * torch.log(yhat) + (1-y) * torch.log(1-yhat))
"""'\ndef BCE_Loss(yhat,y):\n return torch.mean(y * torch.log(yhat) + (1-y) * torch.log(1-yhat))\n'#custom sigmoid + torch.BCELoss 쓰면 오류 발생. 0과 1사이의 범위 아님
#torch.nn.Sigmoid + custom BCE Loss 써도 오류발생 => nan
plt.subplots(2,5,figsize=(20,8))
plt.subplots_adjust(hspace=0.3)
i=1
for epoch in range(200):
#1 yhat
yhat = sig(X@What)
#2 loss
loss = loss_fn(yhat,y)
if epoch % 20 == 0:
plt.subplot(2,5,i)
#plt.plot(X[:,1].data,y,"bo",alpha=0.3)
plt.plot(X[:,1].data,p_i,"r")
plt.plot(X[:,1].data,yhat.data,"g")
plt.xlabel("x")
plt.ylabel("y")
#plt.title("realizations $y_1,\dots,y_{60}$ from $Bern(p_1),\dots,Bern(p_{60})$")
plt.legend(["p","yhat"])
title = "loss : {}".format(round(loss.tolist(),5))
plt.title(title)
i+=1
#3 derivative
loss.backward()
#4 update & clean
What.data = What.data - 0.00005 * What.grad
What.grad = None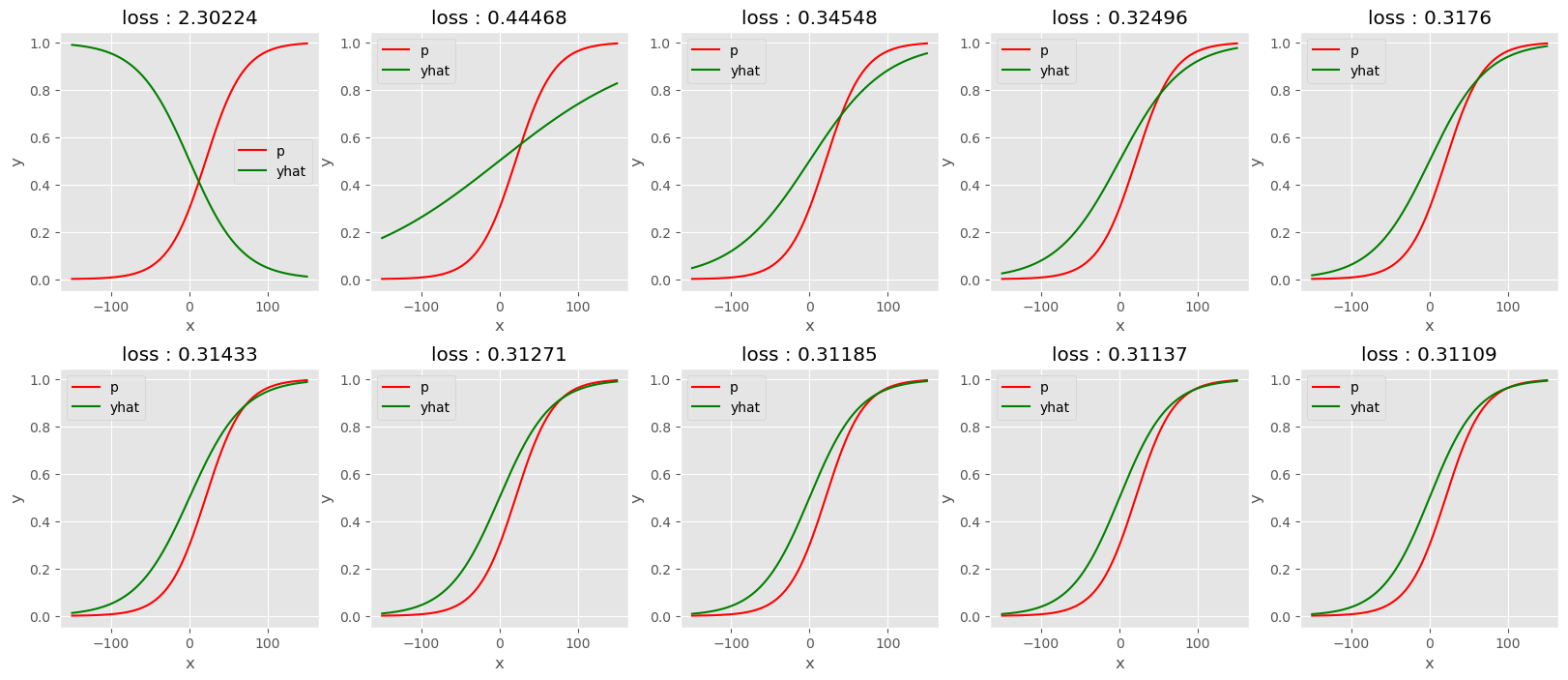
참고링크
1. 로지스틱 회귀 전개
2. 위키피디아 - 로지스틱 회귀
3. ratsgo’s blog