%autosave 20
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
Autosaving every 20 seconds

Background

용어정리

  • (표본)통계량(statistics,sample statistics) : 확률표본으로부터 계산되며 표본의 특성을 나타내는 값.
  • 추정량(estimator) : 모수를 추정할 수 있는 (표본)통계량.
  • 추정값 : 관측한 표본으로부터 계산한 추정량의 값.

정규분포

  • 확률변수 \(X \sim \mathcal{N}(\mu,\sigma^2)\)라 하자.

\[ \begin{aligned} &P(\mu - 2\sigma \leq X \leq \mu + 2\sigma) \approx 0.95 \\ \end{aligned} \]

  • 즉, 평균으로부터 +- 2표준편차인 구간안에 확률변수 X가 값을 가질 확률이 약 95%이다.

  • 이 외에도 표준정규분포표나 다양한 라이브러리를 통하여 확률과 그 확률에 대응하는구간을 구할 수 있다.

통계적 추정

  • 모집단의 특성값인 모수(parameter)가 우리가 알고싶은 것이다.
    • 전북대학교 남학생들의 평균 성적 등등…
  • 통계적 추정 : 확률표본을 사용하여 모집단의 모수 추정 e.g. 모평균,모비율
  • 예를 들자면?
    • 모평균의 추정 : 확률표본으로부터 계산된 표본평균을 추정량으로 사용
    • 모비율의 추정 : 확률표본으로부터 계산된 모비율을 추정량으로 사용.

추정량의 성질

추정량의 임의성

  • 추정량은 표본으로부터 모집단으로부터 표본이 임의적으로(random) 추출되기 때문에 임의성(randomness)를 갖는다.

예시

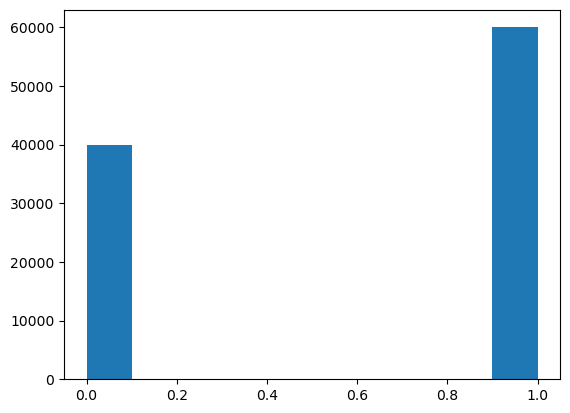
  • 10만명으로 구성된 선거구, A 후보를 지지하는 사람이 6만명, 지지하지 않는 사람이 4만명인 모집단.
  • i.e. 모집단의 크기 \(N=100000\), 지지율 \(\theta = 0.6\)
  1. 모집단 생성
N = 100000 #모집단의 크기
favor = 60000 #지지하는 유권자의 수
opposite = N - favor

P = np.concatenate((np.ones(favor),np.zeros(opposite)),axis=0)
P.shape
(100000,)
plt.hist(P)
plt.show()

  1. 모비율 확인
P.mean()
0.6
  1. 표본 추출
sample = np.random.choice(P,1000,replace=False)
sample[:100]
array([1., 1., 1., 0., 1., 1., 1., 0., 1., 1., 1., 0., 0., 1., 1., 1., 0.,
       1., 1., 0., 0., 1., 1., 0., 1., 1., 0., 0., 0., 1., 1., 0., 1., 0.,
       0., 1., 1., 1., 1., 1., 1., 0., 1., 1., 1., 0., 0., 0., 0., 0., 1.,
       1., 1., 1., 0., 1., 1., 1., 0., 0., 1., 1., 1., 0., 1., 0., 0., 0.,
       0., 0., 1., 0., 1., 0., 1., 0., 0., 1., 1., 0., 1., 1., 0., 1., 0.,
       1., 0., 1., 1., 1., 1., 1., 1., 0., 1., 0., 1., 0., 1., 1.])
  1. 표본비율 계산
hat_theta = sample.mean()
hat_theta
0.59
  1. 표본을 또 한번 추출하여 표본비율 계산
sample = np.random.choice(P,replace=False,size=1000)
hat_theta = sample.mean()
hat_theta
0.615
  • 추출할 때마다 다른 표본이 뽑히므로 추정량의 값(추정값)이 변화한다.
  • 그런데 각각 값들은 모집단의 지지율인 0.6과 아주 많이 차이나진 않는다.

추정량의 평균

  • 추정량은 임의적이기 때문에 표본을 관측하기 전 까지는 알 수 없다.

  • 표본을 관측하면 추정량의 값을 구할 수 있으며 이 값을 추정값(estimate)이라고 한다.

  • 서로다른 여러개의 표본으로부터 각각 계산된 추정값들의 평균\(\bar\theta\)은 어떻게 될까?

  • i.e. \[\bar\theta = \frac{\sum_{i=1}^{1000}\hat\theta_i}{1000}\] (추정값들이 1000개 있다고 하자.)

B = 1000 # 모의실험의 횟수
n = 1000
estimates = pd.DataFrame({'sample_rate':np.zeros(B)})

for i in np.arange(B):
  sample = np.random.choice(P, n, replace=False)
  estimates.loc[i,'sample_rate'] = np.mean(sample)

estimates
sample_rate
0 0.591
1 0.603
2 0.624
3 0.597
4 0.582
... ...
995 0.604
996 0.592
997 0.608
998 0.610
999 0.596

1000 rows × 1 columns

estimates.mean()
sample_rate    0.599952
dtype: float64
P.mean() - estimates.mean()
sample_rate    0.000048
dtype: float64
  • 모의 실험으로부터 얻은 1000개의 추정값들의 평균은 모집단의 지지율 0.6과 매우 유사하다.

\[\bar\theta = \frac{\sum_{i=1}^{1000}\hat\theta_i}{1000} \approx \theta\]

중심극한정리

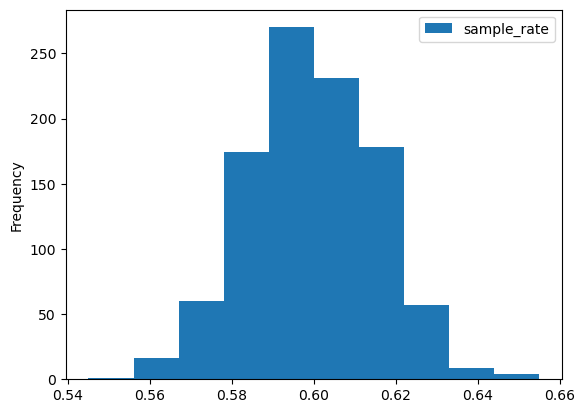
  • 추정량의 분포를 한 번 살펴보자.
estimates.plot.hist()
<AxesSubplot:ylabel='Frequency'>

  • 추정량의 분포는 0.6을 중심으로 종모양의 정규분포처럼 보인다.(잘보면 보임ㅎ)

  • 사실 이는 추정량의 분포가 정규분포를 따른다는 중심극한정리에 의한 내용이다.

::;{.callout-note} #### 중심극한정리(Central Limit Theorem) \(X_1,X_2,\dots,X_n \overset{\text{i.i.d}}{\sim} f_X(x;\mu,\sigma^2)\)라고 하자. 이때 아래와 같은 식이 성립한다. \[\bar X = \frac{X_1 + X_2 + \dots + X_n}{n} \sim \mathcal{N}(\mu,\frac{\sigma^2}{n})\] 일반적으로 \(n \geq 30\)이라고 가정한다. :::

쉽게 풀어쓰자면 - 평균이 \(\mu\)이고, 분산이 \(\sigma^2\) 인 모집단에서 n개의 표본을 추출하는 경우에 n이 충분히 크면( n ≥ 30 ,i.i.d) - 모집단의 분포에 관계없이 표본평균 \(\bar X\)가 정규분포를 따르며 - 그때의 \(E(\bar X) = \mu, Var(\bar X) = \frac{\sigma^2}{n}\)라는 의미이다. - point - 정규분포에서 추출 안해도 정규분포가 됨(모집단이 뭘 따르던 상관 X) - i.i.d가정이 필요(고전적인 CLT) - 다른 CLT도 있는데 그건 같은분포에서 추출 안해도 된다고 함.독립이기만 하면 됨.(wiki 참고 ㄱㄱ)

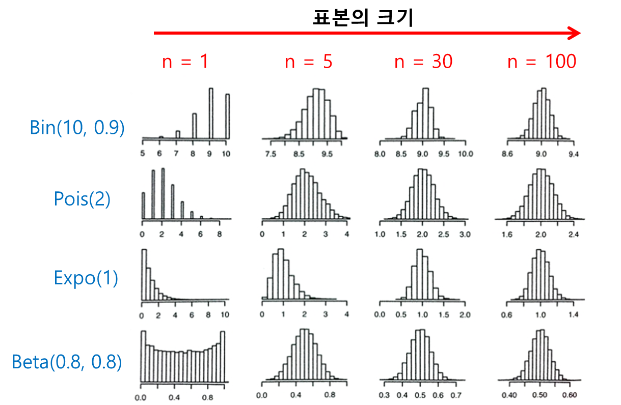
  • 위의 그림이 잘 설명해줌
    • 이항분포던,푸아송이던 … 어떤 분포던지간에 표본의 크기가 충분히 크면
    • 표본평균의 분포는 정규분포임을 확인

추정량의 분포

  • 표본비율(추정량,표본지지율)의 분포를 구해보자.
  • 중심극한정리에 의하면 다음과 같다.

\[ \begin{aligned} \hat\theta \sim \mathcal{N}(\mu(=\theta),\frac{\sigma^2}{n}) \end{aligned} \]

  • 우리가 모르는 것은 우리가 정말 궁금한 \(\mu\)와 분산인 \(\sigma^2\)이다.
  • \(\frac{\sigma^2}{n}\)은 우리가 여러개의 표본으로부터 얻은 추정값들로 어떻게든 구해볼 수 있을 것 같다.
    • \(\hat\theta_1,\hat\theta_2,\hat\theta_3\ \dots\)들의 표본분산으로 구하면 될 것 같다.
    • 여러개의 추정값들로 그러면 \(\mu\)도 구할 수 있는 것 아니냐?라는 의문이 생기는데??
      • 이 경우 \(\mu = E(\hat\theta) \approx\) 표본평균 이라고 생각히가 때문이다.
      • 잘 모르겠다. 하지만 책에서 분산만 일단 전개하므로 여기서도 분산만 가지고 전개.
  • 즉 아래와 같이 표본분산으로 추정할 수 있을 것 같다.

\[ \begin{aligned} &Var(\hat\theta) = \frac{\sigma^2}{n} \approx \frac{\sum_{i=1}^{n}(\hat\theta_i - \bar\theta )^2}{n-1} \text{ (sample variance)}\\ &\Longleftrightarrow Sd(\hat\theta) = \frac{\sigma}{\sqrt{n}} \approx \sqrt{\frac{\sum_{i=1}^{n}(\hat\theta_i - \bar\theta )^2}{n-1}}\text{(sample standard deviation)}\\ &\text{where, } \bar\theta = \frac{1}{n}\sum_{i=1}^{n}\hat\theta_i \end{aligned} \]

  • 결과적으로 표본비율의 분포는 아래와 같다고 할 수 있을 것이다.

\[ \begin{aligned} \hat\theta \sim \mathcal{N}(\mu(=\theta),Sd^2) \end{aligned} \]

구간추정

  • 점추정은 하나의 특정 값으로 모수를 추정하는 방법이였다. 하지만 단점이 있다.
    1. 추정이 얼마나 정확한가,불확실한가를 판단하기가 불가능하다.
    2. 하나의 값을 제시하기에 유연하지 못하고 틀릴 가능성이 높음
  • 이러한 단점을 보완할 수 있는 방법은 구간추정(interval estimation)이
  • 구간추정은 모수에 다한 구간(신뢰구간)과 확률(신뢰도)을 제시하는 추정이며 점추정에 비해 장점이 있음.
    1. 구간을 사용하여 더 유연+견고한 주장을 제시할 수 있음(하나의 값 제시하는게 아니라 ~사이에 있을거다라고 말하는 것이기 때문)
    2. 확률을 제시해 추정이 얼마나 정확한가 제시할 수 있다.(확률 95%,80%로 불확실성을 제시해줄 수 있다.)
  • 목적
    1. 모수 추정
    2. 구간,확률을 제시하여 더 견고한 \(\to\)주장 + 불확실성을 제시하여 추정의 정확도 판단.
  • 구간추정은 어떻게 하는가?(유도해보기)

(알고 있는 사실)
\[\hat\theta \sim \mathcal{N}(\mu,SD^2) \to P(\mu - 2SD \leq \hat\theta \leq \mu + 2SD) = 0.95\text{ (그냥 equal로 놓자.)}\]

(식 살짝 바꾸기)

\[ \begin{aligned} &P(\mu - 2SD \leq \hat\theta \leq \mu + 2SD) = 0.95 \nonumber \\ &\Longleftrightarrow P(-2SD\leq \hat\theta-\mu \leq +2SD) = 0.95 \nonumber \\ &\Longleftrightarrow P(-\hat\theta-2SD \leq -\mu \leq -\hat\theta+2SD) = 0.95 \nonumber \\ &\Longleftrightarrow P(\hat\theta-2SD \leq \mu \leq \hat\theta+2SD) = 0.95 \nonumber \\ &\Longleftrightarrow P(\mu \in [\hat\theta-2SD,\hat\theta+2SD]) = 0.95 \\ &\Longleftrightarrow P(|\mu - \hat\theta| \leq 2SD) = 0.95 \\ \end{aligned} \]

  • 윗 식을 해석해보면?
    • 모수 \(\mu\)가 우리가 관측한 추정량 \(\hat\theta \pm 2SD\)인 구간에 속할 확률이 95%다.
    • 모수 \(\mu\)와 우리가 관측한 추정량 \(\hat\theta\)의 차이가 \(2SD\)보다 작을 확률이 95%다.
  • 결과적으로 모수를 추정함과 동시에 더 유연한 주장 + 불확실성 제시(목적달성).
  • 왜 추정량의 분포를 알아야 했던거지?
    • 확률표본은 모집단으로 부터 임의적으로 추출되기때문에 나타날 수 있는 오차를 추정량의 분포를 이용하여 제시!
  • 용어정리
    • 95%는 신뢰수준
    • 2SD는 표본오차(sampling error)
    • 위에서 나온 구간은 신뢰구간 이라고 함.
    • “모평균 \(\mu\)에 대한 신뢰수준 95%에 대한 신뢰구간은 \([\hat\theta-2SD,\hat\theta+2SD]\)이다”라고 표현.
AVG=  float(estimates.mean()) # B개의 지지율의 평균  
SD = float(estimates.std())   # B개의 지지율의 표준편차

sim_summary = pd.DataFrame({ 'Mean of sample_rates': [AVG], 'SD' : [SD], 'Sampling Error' : [2*SD] })

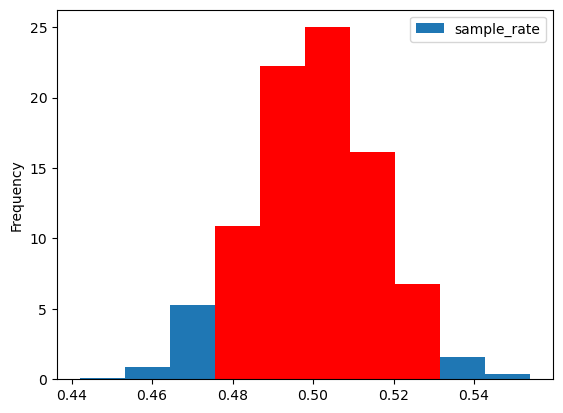
sim_summary
Mean of sample_rates SD Sampling Error
0 0.49992 0.01581 0.031619 
[AVG - 2* SD, AVG + 2*SD ]
[0.46830066758797456, 0.5315393324120261]
# 히스토그램
p= estimates.plot.hist( density=True)

# 모집단의 지지율에서 2SD 만큼 벌어진 구간(95%)은 빨간색으로 
for rectangle in p.patches:
    if rectangle.get_x() >=  (AVG - 2*SD) and rectangle.get_x() <=  (AVG + 2*SD) :
        rectangle.set_facecolor('red')

[AVG - 2* SD, AVG + 2*SD ]
[0.46830066758797456, 0.5315393324120261]
((estimates.sample_rate >= (AVG - 2* SD) ) & (estimates.sample_rate <= (AVG + 2* SD))).mean()
0.96

정리

  • 모집단은 관심이 있는 전체 집단이다,모수는 모집단의 특성값이다.
  • 확률표본은 모집단의 구성원이 표본에 속할 확률을 미리 알고 있으며 그 확률에 따라서 추출한 표본이다.
  • 표본 자료의 분포는 모집단의 분포와 유사하게 나타난다.
  • 추출된 표본으로 부터 얻은 추정량의 값이 모수와 얼마나 차이가 나는지는 알 수가 없다.
  • 하지만 표본의 크기가 커질수록 \(\to\) SD가 감소 \(\to\) 추정량의 값은 모수에 가깝게 나타날 가능성(확률)이 높아진다.
  • 또한 표본의 크기가 크면 추정량의 분포는 정규분포와 매우 유사하다.(by CLT)
  • 따라서 추정량의 분포에 대한 성질을 정규분포의 성질을 이용하여 말할 수 있다.(by CLT)
  • 추정량의 표준편차를 SD 라고 하면 추정량의 값과 모수의 차이가 2*SD 이내일 확률은 약 95% 이라고 말할 수 있다.(by CLT + 정규분포 확률)