import pandas as pd
import numpy as np
import matplotlib.pyplot as plt 

Overview

• 데이터 과학에서 가장 큰 관심은 예측모형을 만드는 것.
• 예측모형을 만들기 전, 여러 변수들 간에 관계를 살펴보는 것은 중요함.
• 여기서는 두 변수사이의 여러가지 관계를 시각화를 통하여 확인해보고, 선형관계를 강도,방향을 나타내는 상관계수를 공부.

두 변수의 관계

• 아버지와 아들사이의 키에 관련된 데이터.
• fheight : 아버지의 키(단위 : inch)
• sheight : 아들의 키(단위 : inch)

url1 = "https://ilovedata.github.io/teaching/bigdata2/data/father-and-son.csv"
father_son_df = pd.read_csv(url1)

father_son_df.head(10)

	fheight	sheight
0	65.04851	59.77827
1	63.25094	63.21404
2	64.95532	63.34242
3	65.75250	62.79238
4	61.13723	64.28113
5	63.02254	64.24221
6	65.37053	64.08231
7	64.72398	63.99574
8	66.06509	64.61338
9	66.96738	63.97944

father_son_df.describe()

	fheight	sheight
count	1078.000000	1078.000000
mean	67.687097	68.684070
std	2.744868	2.814702
min	59.008000	58.507080
25%	65.787735	66.931232
50%	67.766600	68.615820
75%	69.602980	70.465970
max	75.433930	78.364790

father_son_df.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 1078 entries, 0 to 1077
Data columns (total 2 columns):
 #   Column   Non-Null Count  Dtype  
---  ------   --------------  -----  
 0   fheight  1078 non-null   float64
 1   sheight  1078 non-null   float64
dtypes: float64(2)
memory usage: 17.0 KB

• 단위가 inch이므로 바꾸자.

father_son_df = father_son_df * 2.54
father_son_df.head(10)

	fheight	sheight
0	165.223215	151.836806
1	160.657388	160.563662
2	164.986513	160.889747
3	167.011350	159.492645
4	155.288564	163.274070
5	160.077252	163.175213
6	166.041146	162.769067
7	164.398909	162.549180
8	167.805329	164.117985
9	170.097145	162.507778

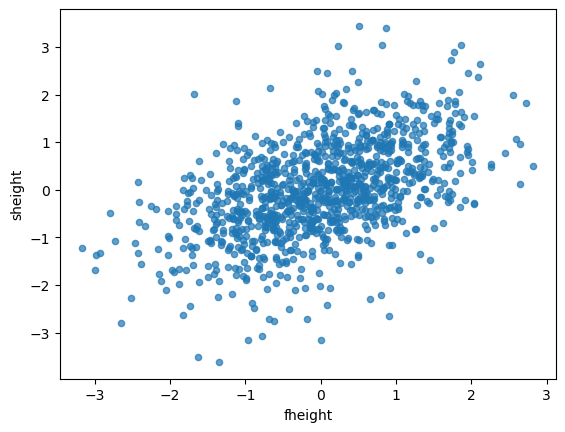
• plot을 해서 두 변수사이의 관계를 살펴보면…

father_son_df.plot.scatter(x='fheight', y='sheight', alpha=0.7)
plt.axvline(x=np.mean(father_son_df.fheight)) 
plt.axhline(y=np.mean(father_son_df.sheight))

<matplotlib.lines.Line2D at 0x23bd8aa6490>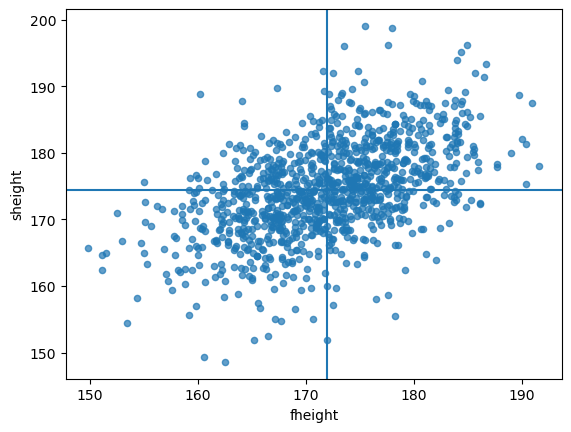

• 아버지의 키가 증가하는 경우 아들의 키도 증가하는 경향을 보이는 것 같다. \(\to\) 선형관계,선형적 비례관계가 있는 것으로 보인다.
• 하지만 예외적인 경우도 충분히 존재한다.
  • 아버지의 키가 커도 아들이 작은 경우.
  • 아버지의 키가 작아도 아들이 큰 경우도 존재한다.

상관계수

• 산점도를 통해서 선형관계가 있음을 짐작할 수 있다.
• 하지만 시각화를 통해서 파악하는 것은 개인에 따라 주관적이며 객관성이 다소 떨어진다.
• 따라서 선형관계의 수치적으로 나타내주는 측도가 필요하며 상관계수가 이러한 측도 중 하나이다.
• 상관계수의 목적 : 두 변수의 선형관계(선형적비례관계)를 수치적으로 나타낸다.(선형관계의 측도)

(상관계수 \(r\))

\[ \begin{aligned} r = \frac{\sum_{i=1}^n(x_i - \bar x)(y_i - \bar y)}{(n-1)SD_xSD_y} \end{aligned} \]

(상관계수 \(r\)) 유도 - 추후 upload

(상관계수 \(r\)의 성질)

• \(-1 \leq r\ \leq 1\)
• \(|r|\)은 선형관계의 강도를 말해준다.
  • \(|r| \approx 1\) : 강한 선형 관계
  • \(|r| \approx 0\) : 약한 선형 관계
• \(|r|\)은 선형관계의 방향을 말해준다.
  • \(|r| >0\) : 양의 선형관계
  • \(|r| <0\) : 음의 선형관계
• \(r \approx 1\) 두 변수는 강한 양의 선형 관계가 있다.
• \(r \approx -1\) 두 변수는 강한 음의 선형관계가 있다.
• \(r \approx 0\) 두 변수는 약한 선형관계가 있다.

(진짜 헷갈리는 것,주의할 것)

• 상관계수 \(r\)은 선형관계에 대한 정보만을 준다. 비선형관계에 대한 정보는 전혀 주지 못한다.
• 자주 헷갈리는 패턴 : \(r = 0\) 두 변수사이의 관계가 없다? \(\to\) X,두 변수사이의 선형관계는 없지만 비선형관계는 존재할 수 있다.

father_son_df.corr()

	fheight	sheight
fheight	1.000000	0.501338
sheight	0.501338	1.000000

• 자기자신끼리는 완벽한(\(r=1\)) 양의 선형 비례관계가 있다.(서로 같은 변수이므로)
• fheight와 sheight는 어느정도 강한 양의 선형관계를 가진다.

예시 - 2차함수

• 상관계수의 값을 좀 더 생각해보기 위해 다음과 같은 데이터를 고려하자.

n=500
x = np.random.normal(0, 5, n)
y = 3.0 * x**2 -10.0 + np.random.normal(0, 10, n)
df_quad = pd.DataFrame({'x':x, 'y':y})
df_quad.plot.scatter(x='x', y='y')

<AxesSubplot:xlabel='x', ylabel='y'>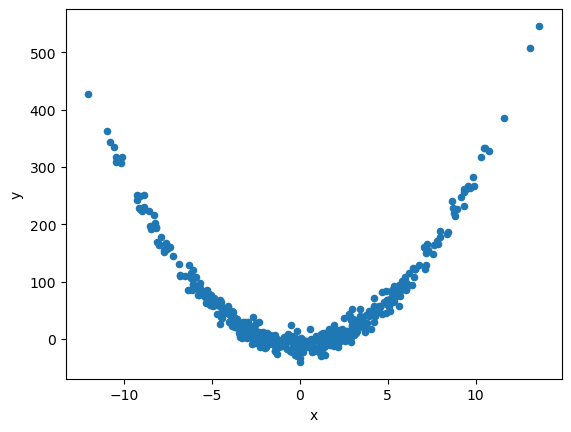

df_quad.corr()

	x	y
x	1.000000	0.049939
y	0.049939	1.000000

• \(x,y\)사이의 상관계수의 \(p \approx 0\)이다.
• 이는 두 변수간에 선형관계가 거의 없다라고 봐도 무방하다.
• 하지만 비선형적인 관계는 존재한다.(2차함수 모양을 그린다.)

변수의 Scailing

• 각각의 변수에 대한 단위(scale)가 다르면?
  1. 비교가 어렵다.
  2. 예측모형의 성능에 영향을 준다.(특히 distance base알고리즘에서 성능저하를 시킨다.)
• 따라서 scale을 통일해줘야 좋다.
• scale의 목적
  • 변수의 단위를 통일 \(\to\) 예측모형 성능 up,변수간의 쉬운 비교

Standardization

• \(\text{standardization} \in \text{변수의 Scailing Method}\)

(Standardization)

\[ \begin{aligned} &z_i = \frac{x_i - \bar x}{SD_x}\\ &\text{Where , }\bar z = 0,SD_z = 0 \end{aligned} \]

• Standardization을 변수들에 적용$\(각 변수들의 평균이 0 표준편차는 1\)$ 변수들이 동일한 scale을 가진다!

Appendix - 상관계수 revision

• 상관계수는 아래와 같이 계산할 수도 있다.

\[ \begin{aligned} &z_i = \frac{x_i- \bar x}{SD_x} , w_i = \frac{y_i-\bar y}{SD_y}\\ &r = \frac{1}{n-1}\sum_{i=1}^nz_iw_i \end{aligned} \]

• 즉,각각의 변수에 해당하는 값들을 모두 Standardization 하는 과정이 포함되어 있다.
• 따라서 두 변수사이의 상관계수는 Scale의 영향을 받지 않는다.
  • 계산과정에서 Standardization으로 Scale을 통일했기 때문이다.

구현

(표준화 하고 상관계수 계산해보기)

def standardize(x):
    return (x-np.mean(x))/np.std(x)

father_son_df_st = father_son_df.apply(standardize,axis=0)
father_son_df_st

	fheight	sheight
0	-0.961726	-3.165498
1	-1.616914	-1.944280
2	-0.995692	-1.898648
3	-0.705132	-2.094156
4	-2.387330	-1.564991
...	...	...
1073	-0.251599	0.735144
1074	1.328444	-0.147981
1075	1.492947	0.221021
1076	1.112144	0.219635
1077	0.954584	-0.593258

1078 rows × 2 columns

father_son_df_st.describe()

	fheight	sheight
count	1.078000e+03	1.078000e+03
mean	-4.050491e-14	2.438217e-14
std	1.000464e+00	1.000464e+00
min	-3.163403e+00	-3.617333e+00
25%	-6.922894e-01	-6.230326e-01
50%	2.897772e-02	-2.425882e-02
75%	6.983112e-01	6.333628e-01
max	2.823607e+00	3.440938e+00

• 평균이 0,분산이 1로 바뀐것을 확인~

father_son_df_st.corr()

	fheight	sheight
fheight	1.000000	0.501338
sheight	0.501338	1.000000

• \(r = 0.503\)로 어느정도 강한 선형관계를 보임.
• 또한 Standardization을 적용하기 전의 값과 상관계수가 같음!(표준화의 영향 X)

father_son_df_st.plot.scatter(x='fheight', y='sheight', alpha=0.7)

<AxesSubplot:xlabel='fheight', ylabel='sheight'>

예제1

• 다음 데이터에서 19세 이상의 성인 남성의 heigt,weight의 관계를 살펴보자.

url2 = "https://ilovedata.github.io/teaching/bigdata2/data/physical_test_2018_data.csv"
physical_data = pd.read_csv(url2, sep=',', encoding = 'utf-8-sig')

physical_01 = physical_data[['TEST_SEX', 'TEST_AGE', 'ITEM_F001', 'ITEM_F002']].rename(columns={'TEST_SEX': 'sex', 'TEST_AGE':'age' ,'ITEM_F001':'height', 'ITEM_F002':'weight'})
physical_01.head(5)

	sex	age	height	weight
0	M	33	159.2	57.2
1	F	48	155.8	52.9
2	M	22	175.2	96.2
3	M	29	178.7	79.4
4	F	31	160.1	50.2

M_19 = physical_01.loc[(physical_01["sex"] == "M") & (physical_01["age"]>=19)]
M_19.head(5)

	sex	age	height	weight
0	M	33	159.2	57.2
2	M	22	175.2	96.2
3	M	29	178.7	79.4
7	M	24	174.9	74.5
15	M	25	175.3	71.3

M_19.plot.scatter(x="height",y="weight",alpha=0.5)

<AxesSubplot:xlabel='height', ylabel='weight'>

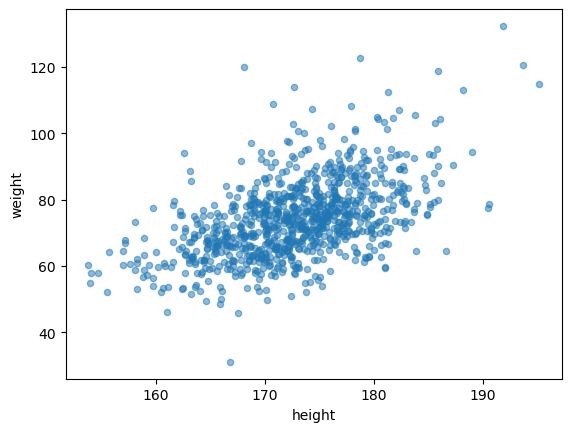
• 음… 양의 선형관계가 있어보인다. 상관계수로 조금 더 자세히 살펴보자.

• 정규분포를 따르는 경우의 산점도와 매우 유사하다. 이는 키와 몸무게의 분포가 정규분포와 매우 유사하기 때문.

• 국민체력 100 데이터는 확률표본이 아니다.

  • from 나무위키 …
  • 체력인증은 만 11세 이상이면 누구나 참여 가능하고, 전국에 있는 체력인증센터에서 무료로 인증 서비스를 제공하고 있다….
  • 체력인증을 받기 위해선 국민체력100의 사이트에 가입해야 하며, 체력측정 신청 전 먼저 문진 검사(PAR-Q)를 통해 체력검사 가능 대상자로 판별돼야 한다.
  • 따라서 우리나라 19세 이상의 모든 남자에 대해서 위의 결론을 일반화 할 수 없다. (확률표본이 아닌 편의표본이기 때문이다.)

M_19[["height","weight"]].corr()

	height	weight
height	1.000000	0.523845
weight	0.523845	1.000000

• height,weight사이의 상관계수 \(r = 0.52\)정도로 어느정도 강한 양의 상관관계가 있다.
• 표준화 하기전과 값이 같다.!(상관계수는 단위의 영향을 받지 않는다!)

예제2

• 다음예제에서 아파트 면적과 가격사이의 관계를 살펴보자

url3 = "https://ilovedata.github.io/teaching/bigdata2/data/seoul_apartment_2019.csv"
apart_2019_1.head(3)
apart_2019_1 = pd.read_csv(url3, encoding="CP949")
apart_2019_2 = apart_2019_1[["신고년도","자치구명","건물면적","층정보","건축년도","건물주용도","물건금액"]]
apart_2019_3 = apart_2019_2.loc[ (apart_2019_2['건물주용도'] == "아파트") & (apart_2019_2['건축년도'] > 0.0)] # 건축연도가 0 보다 큰 아파트만 선택 

apart_2019_4 = apart_2019_3.astype({'층정보': 'int', '건축년도': 'int', '신고년도': 'int'}) # 층과 연도를 정수 형식으로 변환

price = apart_2019_4['물건금액']/1000000            # 거래 가격의 단위를 백만원으로
price = price.astype('int')                         # 거래 가격을 정수 형식으로 변환 
apart_2019_4['price'] = price

# 열이름을 영문으로 변환
apart_2019_5 = apart_2019_4.rename(columns={'신고년도': 'year_sale', '자치구명':'gu','건물면적':'area', '층정보':'floor', '건축년도':'year_built', '건물주용도':'type', '물건금액':'orig_price'})

# 행 인덱스의  초기화
apart_2019 = apart_2019_5[['year_sale', 'gu', 'area','floor','year_built','price']].reset_index(drop=True)

C:\Users\22668\AppData\Local\Temp\ipykernel_28724\2143785989.py:3: DtypeWarning: Columns (1) have mixed types. Specify dtype option on import or set low_memory=False.
  apart_2019_1 = pd.read_csv(url3, encoding="CP949")

apart_2019.shape

(67238, 6)

apart_2019.head(5)

	year_sale	gu	area	floor	year_built	price
0	2019	중구	84.97	15	2017	1390
1	2019	중구	59.94	8	2017	950
2	2019	중구	59.94	18	2002	785
3	2019	중구	59.89	9	2011	990
4	2019	성동구	84.87	12	2007	1450

apart_2019.plot.scatter(x="area",y="price",alpha=0.3)

<AxesSubplot:xlabel='area', ylabel='price'>

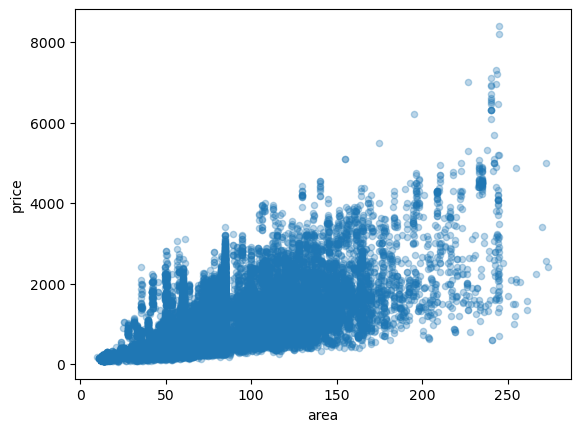
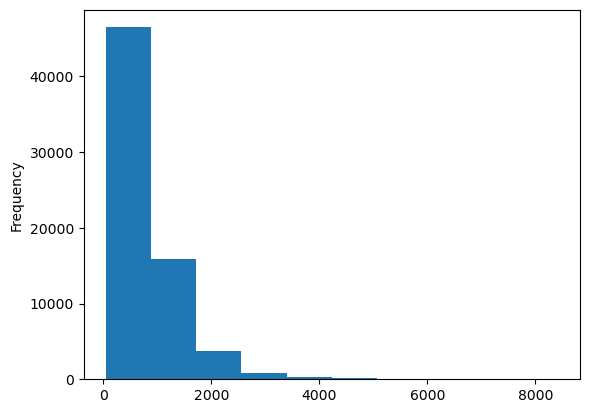
• 전체적으로 면적이 증가하면 가격도 증가하는 경향을 보임 \(\to\) 양의 상관관계를 가질 것처럼 보임(상관계수를 계산해보자.)
• 면적이 커지면 커질수록 price의 변동이 심함을 확인할 수 있음.

apart_2019[["area","price"]].corr()

	area	price
area	1.000000	0.624639
price	0.624639	1.000000

• price,area는 강한 양의 선형관계를 보인다.

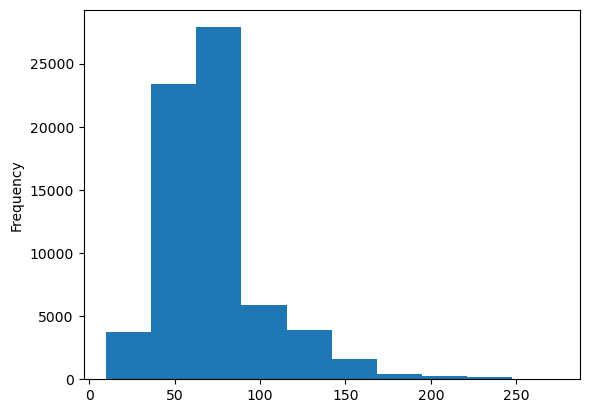
• 추가적으로 price,area 변수를 plotting 해보면?

apart_2019.area.plot.hist()

<AxesSubplot:ylabel='Frequency'>

apart_2019.price.plot.hist()

<AxesSubplot:ylabel='Frequency'>

• 두 변수 모두 오른쪽으로 꼬리가 긴 분포임을 확인할 수 있다.

• 만약 변수를 표준화하고 시각화하면 어떨까?

apart_2019[["area","price"]].apply(standardize,axis=0).plot.scatter(x="area",y="price",alpha=0.3)

<AxesSubplot:xlabel='area', ylabel='price'>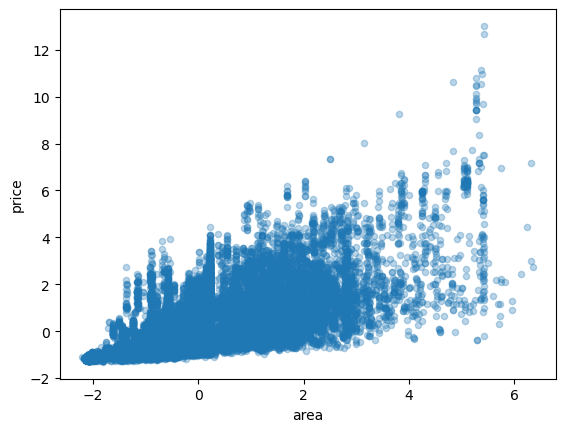

• 표준화 해도 두 변수사이의 관계는 유지된다.

apart_2019[["area","price"]].apply(standardize,axis=0).corr()

	area	price
area	1.000000	0.624639
price	0.624639	1.000000

• 또한 상관계수도 같다.

보충할 내용

• (상관계수 \(r\))유도