from itertools import combinations
P = ['철수', '영이', '둘리', '흥민', '연경']
N = len(P)
n = 3
all_possible_samples = []
all_possible_samples_text = []
for sample in combinations(P, n):
all_possible_samples.append(sample)
txt = ""
for i,name in enumerate(sample):
if i == len(sample) -1:
txt += name
else:
txt+= name + ","
all_possible_samples_text.append(txt)
all_possible_samples_text['철수,영이,둘리',
'철수,영이,흥민',
'철수,영이,연경',
'철수,둘리,흥민',
'철수,둘리,연경',
'철수,흥민,연경',
'영이,둘리,흥민',
'영이,둘리,연경',
'영이,흥민,연경',
'둘리,흥민,연경']통계량의 정확한 분포
우리가 궁극적으로 알고자 하는 것은 모집단의 특성값인 모수이다.
모수를 구하기 위해 우리는 표본으로부터 얻은 표본통계량을 이용한다.
그러므로 표본통계량에 (확률적)성질,특징에 대하여 이해해야 한다.
목적 : 모수를 구하기 위해 표본통계량을 사용하므로 표본통계량을 확률적 성질,특징을 확인해보자.
표본은 모집단으로부터 임의적(random)으로 추출된다.
따라서 표본으로부터 계산한 표본통계량도 random하며 확률변수이다.
그렇다면 표본 통계량의 분포는 어떻게 되는가?
- 가능한 모든 표본통계량의 값과
- 각각의 값에 대응하는 확률을 알아야 한다.
(가능한 모든 표본 통계량의 값 구하기)
from fractions import Fraction
support = {'철수':1, '영이':1, '둘리':0, '흥민':0, '연경':1}
sample_rate = []
for i,sample in enumerate(all_possible_samples):
total = 0
for obj in sample:
total += support[obj]
sample_rate.append(Fraction(total,3))
sample_rate[Fraction(2, 3),
Fraction(2, 3),
Fraction(1, 1),
Fraction(1, 3),
Fraction(2, 3),
Fraction(2, 3),
Fraction(1, 3),
Fraction(2, 3),
Fraction(2, 3),
Fraction(1, 3)](각각의 표본통계량에 대응하는 확률 구하기) - 아래의 데이터 프레임은 가능한 모든 표본으로부터 계산한 통계량과 각각의 표본이 뽑힐 수 있는 확률을 나타낸다.
sample_rate_dist = pd.DataFrame({"sample(outcome)" : all_possible_samples_text, "sample_rate" : sample_rate,"prob" : [0.1 for i in range(len(sample_rate))]})
sample_rate_dist| sample(outcome) | sample_rate | prob | |
|---|---|---|---|
| 0 | 철수,영이,둘리 | 2/3 | 0.1 |
| 1 | 철수,영이,흥민 | 2/3 | 0.1 |
| 2 | 철수,영이,연경 | 1 | 0.1 |
| 3 | 철수,둘리,흥민 | 1/3 | 0.1 |
| 4 | 철수,둘리,연경 | 2/3 | 0.1 |
| 5 | 철수,흥민,연경 | 2/3 | 0.1 |
| 6 | 영이,둘리,흥민 | 1/3 | 0.1 |
| 7 | 영이,둘리,연경 | 2/3 | 0.1 |
| 8 | 영이,흥민,연경 | 2/3 | 0.1 |
| 9 | 둘리,흥민,연경 | 1/3 | 0.1 |
- 크기가 5인 모집단에서 크기가 3인표본을 추출할 때, 특정한 하나의 표본이 추출될 확률(단,단순임의추출을 했다고 가정)?
- 가능한 표본이 \({10}\choose{3}\) = 10이고
- 단순임의추출 : 각표본을 추출할 확률은 모두 동일하므로 \(0.1\)
\[ \begin{aligned} &P(철수,영이,둘리) = P(철수,영이,연경) = \dots = P(둘리,흥민,연경) = 1 \\ &\Leftrightarrow10P = 1 \\ &\Leftrightarrow P = 0.1 \end{aligned} \]
- 확률과정론으로부터 얻은 지식…
- \(P(\hat{\theta} = \frac{2}{3}) = P(\{\omega : \hat{\theta}^{-1}(\omega) = \frac{2}{3} \})= 0.6\)
- i.e. 표본통계량 = \(\frac{2}{3}\)이 가능한 outcome(sample)은 총6가지 경우이며 확률은 각각 1이므로 \(6 \times 0.1 = 0.6\)
- \(P(\hat{\theta} = 1) = P(\{\omega : \hat\theta^{-1}(\omega) =1\}) = 0.1\)
- i.e.(표본통계량 = \(1\)이 가능한 outcome은 1가지 경우여서 확률은 0.1
- \(P(\hat{\theta} = \frac{1}{3}) = P(\{\omega : \hat{\theta}^{-1}(\omega) = \frac{1}{3} \})= 0.3\)
- i.e. 표본통계량 = \(\frac{1}{3}\)이 가능한 outcome(sample)은 총3가지 경우이며 확률은 각각 1이므로 \(3 \times 0.1 = 0.3\)
- \(P(\hat{\theta} = \frac{2}{3}) = P(\{\omega : \hat{\theta}^{-1}(\omega) = \frac{2}{3} \})= 0.6\)
- 따라서 정확한 \(\hat\theta\)의 분포는
| \(\hat\theta\) | \(\frac{1}{3}\) | \(\frac{2}{3}\) | 1 |
|---|---|---|---|
| \(P\) | 0.3 | 0.6 | 0.1 |
통계량의 경험적 분포
사실 통계량의 정확한 분포를 구하는 것은 불가능하다.
- 실제 문제에서는 모집단 자체를 정확히 모를 뿐더러
- 정확히 안다고 할지라도 모집단의 크기가 너무 크면 불가능하다.
모집단의 크기가 너무 크다.
\(\to\) 가능한 모든 표본의 수가 \({N}\choose{n}\) 개이다.
\(\to\) 가능한 모든 표본으로부터 통계량을 구하는 것은 컴퓨터로도 처리하기 어렵다정확한 표본통계량의 분포를 구하기 힘드니까 근사적으로라도 구할 수 없을까?
목적
- 표본통계량의 정확한 분포는 구할 수 없으므로 표본통계량의 분포를 (근사적으로) 구한다.
- 근사적으로 구한 분포로부터 표본통계량의 확률적 성질,특징을 알아볼 수 있다.
How? : 경험적 분포를 구한다.
(경험적 분포를 구하는 과정)
- 문제 : 모집단의 크기 N = 10000이고 표본의 크기 n=100으로 할 때, 표본통계량(지지율)의 분포는 어떻게 되는가? 1. 모집단으로 부터 크기가 100인 표본을 임의추출 한다.(기억,랜덤샘플링,임의추출) 2. 표본으로부터 표본통계량 \(\hat\theta\)을 계산하고 기록한다. 3. 1,2,를 여러번 반복한다. - 일반적으로 500이상 - 예를 들어 500번 반복하면 \(\hat\theta_1,\hat\theta_2,\hat\theta_3...\hat\theta_{500}\)을 얻었을 것이다. 4. 위에서 얻은 여러 개의 표본통계량으로 부터 경험적 분포를 구한다.
- 위와 같은 과정을 모의실험이라고 하며 모의실험을 통하여 얻은 분포를
경험적 분포라 한다. - 표본통계량의 경험적 분포는 정확한 분포와 매우 유사하다.
- 따라서 표본통계량의 정확한 분포를 구할 수 없는 경우 표본통계량의 경험적 분포를 통하여 확률적 성질,특징을 알아볼 수 있다.
구현
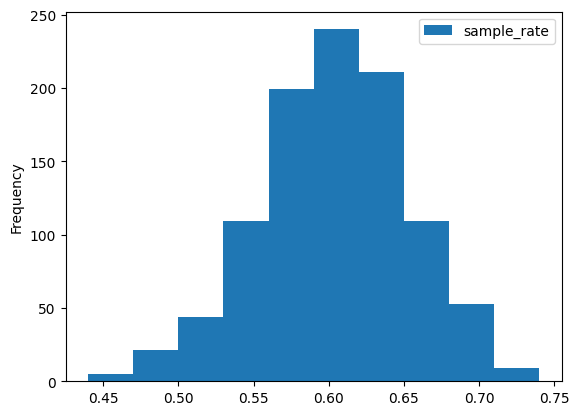
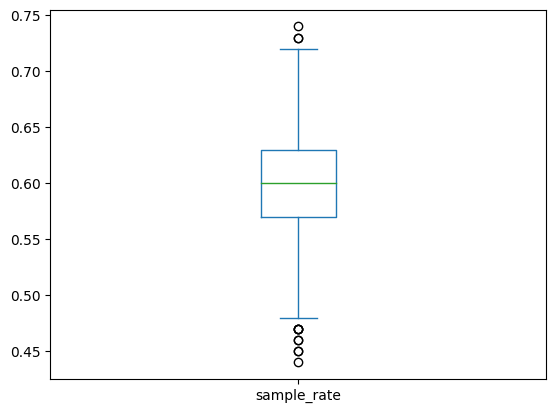
- 지지율이 60%인 모집단이 있다고 할 때
- 모의실험을 통해 크기가 100인 표본지지율의 경험적 분포를 구해보자.
- 모집단 \(P\)는 np.array이다.
- 따라서 단순임의추출하려면 np.random.choice사용
B=1000
n=100
simulation_sample_rate = pd.DataFrame({"sample_rate":np.zeros(B)})
for i in np.arange(B):
sample = np.random.choice(P,n,replace=False)
simulation_sample_rate.loc[i,"sample_rate"] = np.mean(sample)
simulation_sample_rate| sample_rate | |
|---|---|
| 0 | 0.47 |
| 1 | 0.62 |
| 2 | 0.55 |
| 3 | 0.59 |
| 4 | 0.63 |
| ... | ... |
| 995 | 0.60 |
| 996 | 0.61 |
| 997 | 0.59 |
| 998 | 0.55 |
| 999 | 0.60 |
1000 rows × 1 columns