import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

%autosave 20
Autosaving every 20 seconds

부트스트랩

  • 지난번에 한 구간추정은 이런 과정이였음.

    • 모집단으로부터 여러번 임의추출하여 여러개의 표본을 만들고
    • 각각의 표본으로부터 추정량의 값인 추정값를 계산하고
    • 계산된 추정값들로부터 추정량의 표준편차(또는 분산)을 구하고 + 중심극한정리(CLT)의 이론적 백업을 바탕으로
    • 모수 \(\mu\)에 대한 95% 신뢰구간을 제시
      1. \(\mu\) 는 \(\hat\theta \pm 2SD\)인 구간에 95%확률로 속할 것이다.
      2. \(\mu - \hat\theta\)의 차이는 95%확률로 \(2SD\)보다 작을 것이다.

  • 하지만 실전에서는 모집단에서 표본은 단 한번 추출함(시간과 비용)

  • 그러면 여러개의 추정값들을 얻을 수 없기에 추정량의 표준편차(\(SD\))를 못 구하는데 어떻게 해야할까?

  • 부트스트랩(bootstrap)을 통해 추정량의 표준편차를 구할 수 있음.

  • 부트스트랩의 목적 : 하나의 샘플만 주어진 상황에서 추정량의 표준편차\(SD\)를 구하여 구간추정을 할 수 있도록 하자.

  • 부트스트랩의 idea : 표본을 모집단처럼 이용하자!

그림

(부트스트랩 과정) 1. 표본으로부터 재추출(resampling)을 통해 재표본(resample)을 만든다. 2. (부트스트랩) 추정치를 구하고 기록한다. 3. 1.2를 여러번 반복한다. 4. 추정량의 분포를 근사하는 경험적 분포와 추정량의 표준편차 \(SD\)를 여러개의 추정치로부터 계산한다.!

(유의해야 할 점) - 재추출(resampling)만 유의하면 된다. - 재추출은 표본으로부터 복원추출 - 표본과 재표본의 크기는 같아야 함.

Bootstrap 실습

모집단 생성

N = 100000  #모집단의 크기
theta = 0.5 #모비율 (지지율)

favor = int(N * theta) # 지지하는 유권자 수
opposite = N - favor
P = np.concatenate((np.ones(favor),np.zeros(opposite)))

모집단에서 하나의 확률표본만 있다고 가정

n = 1000
one_sample = np.random.choice(P,n,replace=False)

표본지지율은 ?

hat_theta = one_sample.mean()
hat_theta
0.507

부트스트랩 ㄱㄱㅆ

  • 부트스트랩 과정 recap
    • 표본으로부터 복원추출하여 크기=n인 재표본을 생성
    • 생성된 재표본으로부터 추정량 계산
    • 이전 과정2개를 반복하여 여러개의 추정값들 계산
    • 추정값들의 분포가 추정량의 분포와 거의 비슷하다!
      • 추정량의 분산도 여기서 구하면 되겠지?
B = 1000 #부트스트랩 모의실험 횟수. 추정값들의 갯수와 동일

bootstrap_estimates = pd.DataFrame({"resample_estimate":np.zeros(B)}) # B개의 추정치를 저장할 데이터프레임 확보

for i in np.arange(B):
    resample = np.random.choice(one_sample,n,replace=True)
    bootstrap_estimates.loc[i,"resample_estimate"] = resample.mean()
bootstrap_estimates.head(10)
resample_estimate
0 0.532
1 0.504
2 0.478
3 0.491
4 0.497
5 0.512
6 0.508
7 0.523
8 0.507
9 0.484

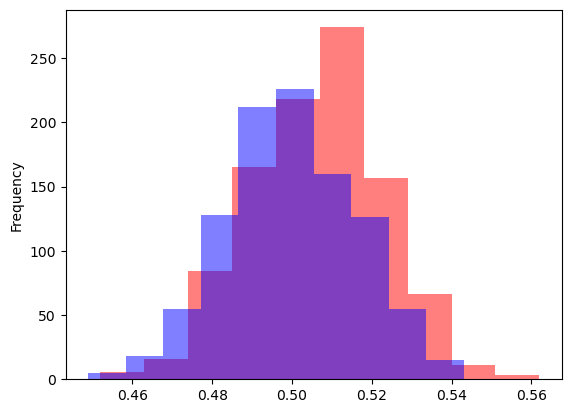
여러번 sampling vs 여러번 resampling(부트스트랩)

B = 1000

estimates = pd.DataFrame({"sample_rate" : np.zeros(B)})

for i in np.arange(B):
  sample = np.random.choice(P, n, replace=False)
  estimates.loc[i,'sample_rate'] = np.mean(sample)

estimates.head(10)
sample_rate
0 0.501
1 0.488
2 0.503
3 0.486
4 0.478
5 0.484
6 0.498
7 0.499
8 0.496
9 0.516 
bootstrap_estimates.resample_estimate.plot.hist(alpha=0.5,color="red")
estimates.sample_rate.plot.hist(alpha=0.5,color="blue")
<AxesSubplot:ylabel='Frequency'>

\(SD\)구하기

  • \(SD\)는 \(Std(\hat\theta)\)를 근사적으로 구한 값이라 하자.(이전에는 sampling을 여러번해서 구했었음)
SD = float(bootstrap_estimates.std())
round(SD,3)
0.016

참고 - 여러번 sampling한 추정량의 분포로부터 구한 SD는?

SD2 = float(estimates.std())
round(SD2,3)
0.016
  • 매우매우 유사하다.

참고 - 중심극한 정리에 의한 이론적인 추정량의 분산은?

\[ \begin{aligned} &Var(\hat\theta) = \frac{\sigma^2}{n} \\ &Std(\hat\theta) = \sqrt{\frac{\sigma^2}{n}} \\ \end{aligned} \]

theta_hat_std = (P.var()/n)**(0.5)
theta_hat_std.round(3)
0.016
  • 매우매우 유사하다.

Bootstrap을 사용한 구간추정

SD활용

lower_bound = hat_theta - SD * 2
upper_bound = hat_theta + SD * 2
lower_bound,upper_bound
(0.4747162808443246, 0.5392837191556754)

Percentile 사용

lower_bound = float(bootstrap_estimates.quantile(0.025))
upper_bound = float(bootstrap_estimates.quantile(0.975))
lower_bound,upper_bound
(0.475, 0.536025)

신뢰구간 해석

  1. 95%의 확률로 신뢰구간이 모수를 포함한다. (\(\hat\theta\)가 확률변수, \(\theta\)는 고정된 상수,신뢰구간이 바뀐다. 고전적인 통계의 관점)
  2. 95%의 확률로 모수가 신뢰구간에 포함된다. (\(\theta\)가 확률변수, \(\hat\theta\)는 고정된 상수,신뢰구간은 고정.베이지안 관점)

세부적으로 이렇게 적을 수 있지만 사실 차이가 이해하기 어려우므로 95% 신뢰구간에 모수가 포함되었을 가능성이 95%라 생각해도 큰 문제는 없다.

예제 : 중앙값의 신뢰구간 구하기

url1 = "https://ilovedata.github.io/teaching/bigdata2/data/seoul_bike_201909_3.csv"
bike = pd.read_csv(url1, encoding="CP949")
bike
자전거번호 대여일시 대여 대여소번호 대여 대여소명 대여거치대 반납일시 반납대여소번호 반납대여소명 반납거치대 이용시간 이용거리
0 SPB-17003 2019-09-28 16:10:55 368 SK 서린빌딩 앞 4 2019-09-28 17:03:32 2002 노들역 1번출구 14 52 8940.0
1 SPB-14405 2019-09-28 16:48:16 2024 상도역 1번출구 3 2019-09-28 17:03:44 2002 노들역 1번출구 18 15 1910.0
2 SPB-18431 2019-09-28 16:59:54 2002 노들역 1번출구 10 2019-09-28 17:03:57 2002 노들역 1번출구 10 2 30.0
3 SPB-04853 2019-09-28 15:31:49 207 여의나루역 1번출구 앞 32 2019-09-28 17:10:12 2002 노들역 1번출구 19 98 9610.0
4 SPB-11122 2019-09-28 15:35:41 207 여의나루역 1번출구 앞 14 2019-09-28 17:10:37 2002 노들역 1번출구 18 90 9450.0
... ... ... ... ... ... ... ... ... ... ... ...
407584 SPB-24072 2019-09-12 08:56:34 240 문래역 4번출구 앞 9 2019-09-12 09:03:37 99999 영남단말기정비 2 6 720.0
407585 SPB-16130 2019-09-18 10:13:09 99999 영남단말기정비 1 2019-09-18 11:38:30 99999 영남단말기정비 1 85 40.0
407586 SPB-03728 2019-09-25 08:00:28 2183 동방1교 7 2019-09-25 08:54:02 99999 영남단말기정비 5 53 12910.0
407587 SPB-08928 2019-09-30 07:49:27 2183 동방1교 10 2019-09-30 09:42:27 99999 영남단말기정비 7 2 0.0
407588 SPB-06988 2019-09-30 09:58:43 99999 영남단말기정비 5 2019-09-30 13:01:26 99999 영남단말기정비 5 182 10.0

407589 rows × 11 columns

bike2 = bike[["이용시간","이용거리"]]
bike2
이용시간 이용거리
0 52 8940.0
1 15 1910.0
2 2 30.0
3 98 9610.0
4 90 9450.0
... ... ...
407584 6 720.0
407585 85 40.0
407586 53 12910.0
407587 2 0.0
407588 182 10.0

407589 rows × 2 columns

bike2.describe()
이용시간 이용거리
count 407589.000000 407589.000000
mean 30.156827 4253.336228
std 32.065934 5782.673901
min 1.000000 0.000000
25% 8.000000 1200.000000
50% 18.000000 2380.000000
75% 43.000000 5130.000000
max 2479.000000 153490.000000 
n = 1000

one_sample = bike2.sample(n=n,replace=False,random_state = 13312)
one_sample.head(10)
이용시간 이용거리
50771 25 1830.0
179510 20 3670.0
167844 8 1180.0
244482 3 210.0
102805 9 1330.0
330458 15 3090.0
91162 3 730.0
22447 6 1940.0
348599 16 1350.0
387639 15 2270.0 
one_sample.describe()
이용시간 이용거리
count 1000.000000 1000.000000
mean 28.150000 3923.110000
std 28.664598 4723.684348
min 1.000000 0.000000
25% 8.000000 1247.500000
50% 18.000000 2345.000000
75% 41.000000 5040.000000
max 321.000000 70890.000000 
B = 1000
n = 1000

bootstrap_estimates = pd.DataFrame({"time_estimate":np.zeros(B),"distance_estimate":np.zeros(B)})
for i in np.arange(B):
    resample = one_sample.sample(n=n,replace=True,random_state = i)
    bootstrap_estimates.loc[i,"time_estimate"] = np.median(resample["이용시간"])
    bootstrap_estimates.loc[i,"distance_estimate"] = np.median(resample["이용거리"])
bootstrap_estimates.head(10)
time_estimate distance_estimate
0 18.0 2305.0
1 17.0 2330.0
2 18.0 2365.0
3 18.0 2410.0
4 19.0 2330.0
5 18.0 2355.0
6 17.0 2310.0
7 17.0 2320.0
8 17.0 2315.0
9 18.0 2375.0 
lower_bound = float(np.quantile(bootstrap_estimates[["time_estimate"]],0.025))
upper_bound = float(np.quantile(bootstrap_estimates[["time_estimate"]],0.975))
lower_bound,upper_bound
(16.5, 20.0)
lower_bound = float(np.quantile(bootstrap_estimates["distance_estimate"],0.025))
upper_bound = float(np.quantile(bootstrap_estimates["distance_estimate"],0.975))
lower_bound,upper_bound
(2180.0, 2530.25)
bike2 = bike[ ["이용시간","이용거리"] ].rename(columns={"이용시간":"time", "이용거리":"distance"})
n = 1000 # 표본의 크기

one_sample = bike2.sample(n=n, replace=False, random_state=13312)
one_sample



B = 1000    # 붓스트랩 모의실험의 횟수

bootstrap_estimates = pd.DataFrame({'time_boot':np.zeros(B), 'distance_boot':np.zeros(B)})

for i in np.arange(B):
  boot_sample = one_sample.sample(n=n, replace=True, random_state=i)
  bootstrap_estimates.loc[i,'time_boot'] = np.median(boot_sample.time)
  bootstrap_estimates.loc[i,'distance_boot'] = np.median(boot_sample.distance) 

bootstrap_estimates
time_boot distance_boot
0 18.0 2305.0
1 17.0 2330.0
2 18.0 2365.0
3 18.0 2410.0
4 19.0 2330.0
... ... ...
995 17.5 2305.0
996 19.0 2360.0
997 19.0 2315.0
998 17.0 2320.0
999 19.0 2375.0

1000 rows × 2 columns

뭐야 왜 강의자료랑 다르게 나옴 ..?